Frequency-Modulated Continuous-Wave Radar
Table of Contents
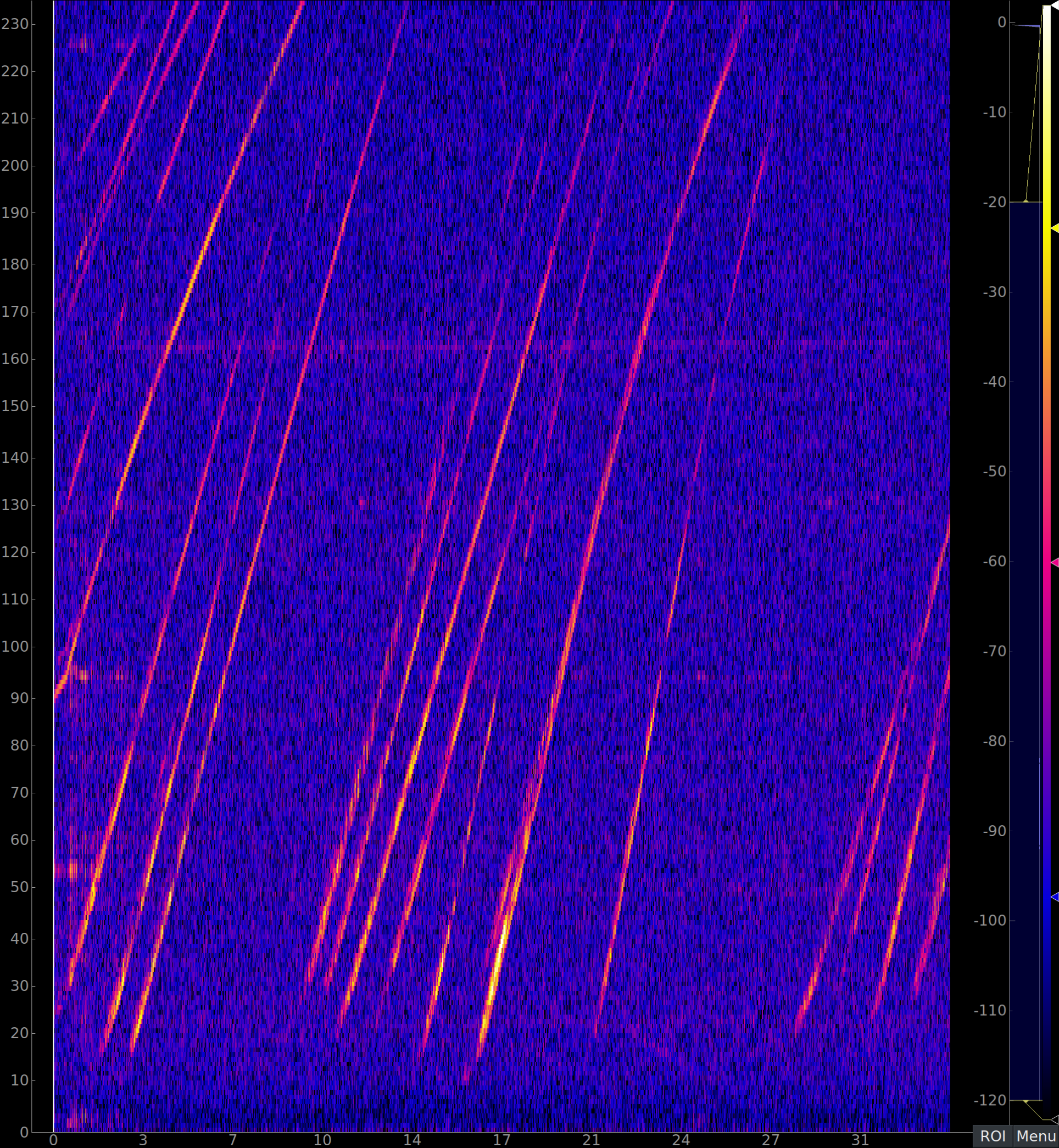
Figure 1: Real-time range detection performed by radar. Distance (y-axis) is in meters and the time (x-axis) is in seconds. Magnitude is in dBFS relative to the max ADC input.
1. Introduction
This blog presents the key details of an FPGA-based radar I developed and built, including a summary of the relevant physics followed by more in-depth descriptions of the various hardware components and related FPGA and PC (linux) programming. It focuses on design and implementation details rather than how to use this radar. For usage information see the README. My formal education is in physics, not electrical engineering or software programming. But after a few years trading financial derivatives I decided that I wanted to do something more fun and challenging, and I chose this project to develop several areas of technical knowledge — including electrical engineering and FPGA programming — and apply them in a practical way.
I was originally motivated by an excellent design for a radar by Henrik Forsten that provides a valuable description of many key components. My debt to Henrik and appreciation of his work are great. Building on what he did, I created a design that uses an FPGA in a much more significant way — to perform all major real-time processing of the radar reception data — and wrote the interfacing host PC code from scratch. This met my twin goals of being able to configure hardware for large-volume data processing and developing a diverse set of electrical engineering and programming skills.
The biggest and most rewarding challenge in this project involved the FPGA gateware design and programming (described here). Other aspects of the project — characterizing the radar physics, designing and configuring elements of the printed circuit board (PCB) to implement numerous sub-processes and to avoid or eliminate signal problems, simulating and designing the distributed microwave structures, and programming the PC to interface with the FPGA and other hardware elements — were also uniquely valuable. In particular:
- I've completely rewritten the FPGA code so that all the signal processing is now performed in real time on the FPGA. I've done this without changing the actual FPGA device used. I've also added tests and some formal verification to accompany the new code.
- I've written a high-level Python interface to the OpenEMS electromagnetic wave solver and simulated and designed the microwave parts of the radar using this tool. These simulations are described in the RF Simulation section of this post.
- I've rewritten the host PC software from scratch to accommodate the new FPGA code.
- I've redone the PCB layout from scratch in order to modify the design for a deprecated part.
- I designed and 3D printed horn antennas and a mount for the radar.
- I've added a few analog simulations of relevant parts of the PCB using Ngspice.
The full project code is open source and can be viewed on GitHub. I hope you gain some benefit from what follows. Please do not hesitate to contact me if you have any questions.
2. Miscellaneous Notes
Several preliminary comments about this post are in order.
Although I've put a lot of time into this project, it is still a work in progress. In particular, there have been two major iterations of the hardware design, referred to as rev1 and rev2 (both revisions are maintained in the source code repository). All results presented in this post are from rev1 because I have not yet built rev2. However, these results pointed to a few shortcomings that I designed rev2 to fix. Because this post is meant as a description of the right way to do things, it presents the design considerations for rev2. In several instances, however, I have made references to aspects of rev1 in order to explain shortcomings in certain results.
Finally, a number of sections go into a considerable amount of detail. While I believe these sections are very valuable, I don't expect everyone to read them in full, so I've placed a link at the beginning of them to allow the reader to jump to the next high-level section. Still, the detail's there and I encourage you to read it.
3. Overview
At a very high level, a radar (depending on the technology used) can detect the distance to a remote object, the incident angle to that object, the speed of that object, or some combination of these. This radar currently just detects distance. The hardware supports angle detection too (and Henrik's version does this), but at this stage I have not yet written the code for that.1
Figures 3 and 4 show what the radar looks like with the 3D-printed antennas and mount.
Figure 1 shows the output produced when observing cars on a highway from an overhead bridge.
Broadly, the radar works by emitting a frequency ramp signal that reflects off a remote object and is detected by a receiver. Because the transmitted signal travels through air at the speed of light and its frequency ramps at a known rate, the frequency difference between the transmitted and received signals can be used to determine the distance to the remote object.
4. Physics
4.1. Operating Principle
The distance to a remote object is
| (4.1.1) |
where
The ramp slope and duration are explicitly programmed. So, by finding the frequency difference between the transmitted and received signals, we can find the time difference and thus the distance:
| (4.1.2a) | ||||
| (4.1.2b) |
To find the frequency difference we note that the transmitted signal has the following form (I've restricted
| (4.1.3a) | ||||
| (4.1.3b) | ||||
| (4.1.3c) |
where
The received signal is just a time-delayed copy of the transmitted signal with a different amplitude. The amplitude changes because energy is lost as the wave propagates through air and the signal is amplified by the receiver. Energy is proportional to the amplitude squared. The expression for the received signal is
| (4.1.4a) | ||||
| (4.1.4b) | ||||
| (4.1.4c) |
We can also write this expression as
| (4.1.5) |
where
| (4.1.6a) | ||||
| (4.1.6b) |
The product of two sine functions can be equivalently represented as
| (4.1.7) |
In other words, as a combination of a sinusoid of the frequency sum and a sinusoid of the frequency difference. It's precisely the frequency difference that we want. Moreover, the frequency sum will be much higher than the frequency difference (about 4 orders of magnitude in our case). As a result, the circuitry that we use to pick up the difference frequency won't detect the sum frequency. Using this knowledge, we see that if we multiply the transmitted and received signals we get
| (4.1.8a) | ||||
| (4.1.8b) | ||||
| (4.1.8c) |
So, using a Fourier transform on the mixer output will tell us the frequency difference and thus the distance.
4.2. Range
It's possible to relate the range of a remote object to the power received at a reception antenna using something known as the radar range equation. I've derived this equation in the range equation derivation section. The resulting equation is
| (4.2.1) |
All of these variables except reception power are constant and reasonably easy to calculate. They are presented in Table 6.
(See the power amplifier section for how the transmitted power was determined, and the horn antenna section for the antenna gain.)
Figure 6: Values in range equation.
This leaves us with a function relating range to received signal power. For a reason that will be clear momentarily, we've used received signal power as the dependent variable in Figure 7.
In the maximum and minimum received power sections, we derive the receiver power range as a function of the measured difference frequency. This frequency can be directly related to the distance using Eq. (4.1.2b). Although we can change the ramp duration and frequency bandwidth to our liking, for this calculation I'll use the software defaults of
The visible range corresponds to the range where the actual received power is between the minimum and maximum detectable powers. Additionally, we're restricted to distances corresponding to frequencies less than the Nyquist frequency (
It is important to note that this visible range (and the calculations performed in the minimum and maximum received power sections) correspond to just one possible radar configuration. For instance, it is possible to reconfigure the radar to work for longer ranges without making any hardware or FPGA modifications.
From the Operating Principle section (specifically, Eq. (4.1.2b)), we see that we can can perform some combination of decreasing
This plot shows that we should be able to detect remote objects out to
Finally, it's worth mentioning that in the old version of the PCB that I'm currently using for testing, the noise floor is higher than it should be (the new version is designed and should fix this issue, but is not yet ordered and assembled). I'm measuring a noise floor of
4.2.1. Range Equation Derivation
Next high-level section: PCB Design
Most of the steps in this derivation are identical to the derivation for the well-known Friis transmission formula.
Start by imagining that our transmission antenna is isotropic. The power density at some remote distance
| (4.2.1.1) |
where
| (4.2.1.2) |
At this distance,
| (4.2.1.3a) | ||||
| (4.2.1.3b) |
where
We now imagine the remote object simply as a remote isotropic antenna with transmission power given by the reflected power shown above. And we use the same method as the first step to find the power density available at the reception antenna:
| (4.2.1.4a) | ||||
| (4.2.1.4b) |
To find the actual received power, we multiply the power density by the reception antenna's effective aperture and efficiency:
| (4.2.1.5a) | ||||
| (4.2.1.5b) | ||||
| (4.2.1.5c) |
This is the final result. We could equivalently rearrange our equation in terms of the distance,
| (4.2.1.6) |
In our case the transmission and reception antennas are identical, so the equation simplifies to
| (4.2.1.7) |
5. PCB Design
Figure 10 shows a simplified implementation of how the radar PCB works. The data processing (shown as part of the FPGA section) is more flexible in the actual implementation. Notably, the user can decide what processing to perform and whether this processing should be performed on the FPGA or on the host PC (see the FPGA and software sections for more detail).
A frequency synthesizer generates a sinusoidal signal that ramps in frequency from
5.1. Transmitter
The transmitter is responsible for generating a frequency ramp that is transmitted through space by an antenna and coupled back into the receiver. An ADF4158 frequency synthesizer and voltage-controlled oscillator (VCO) together generate the ramp signal. A resistive splitter then divides the signal, sending a quarter of the input power to the power amplifier for transmission and another quarter back to the frequency synthesizer (see the frequency synthesizer section). The power amplifier amplifies the signal, most of which is sent to the antenna for transmission. The remainder is coupled back to the receiver. The transmitter is shown in Figure 11.
5.1.1. Frequency Synthesizer
Next high-level section: Receiver
The ADF4158 frequency synthesizer is based on a fractional-N phase-locked loop (PLL) design. The device is highly configurable, which can be viewed in the datasheet. Chapter 13 of the Art of Electronics (3d ed.) (AoE) provides an excellent description of how a PLL works. I explain the relevant points here. The frequency synthesizer consists of a phase detector and VCO (our VCO is an external component). Figure 12 shows a block diagram of the synthesizer (note that this diagram has been adapted from AoE).
The phase detector, as the name suggests, outputs a voltage signal which corresponds to the difference in phase between two input frequencies. The VCO generates a frequency that is proportional to an input voltage. (Disregard the frequency divider blocks for a minute. We'll get back to them.)
All we've done so far is take
| (5.1.1.1a) | ||||
| (5.1.1.1b) |
By setting
5.1.2. Resistive Power Splitter
Next high-level section: Receiver
A resistive splitter is a circuit that splits the power at its input between two outputs. The splitter used in this design splits the power evenly between both outputs, though there are splitters designed for uneven splits. Because the splitter is resistive, it loses half of the input power to heat. This leaves
Our requirements for the splitter or divider are not very demanding. The bandwidth is limited and the power available to the splitter is enough for each output even with the loss. Also, the power is low enough that the heat dissipation doesn't pose a problem. Therefore, using either of these devices would have worked fine. I've opted to use the splitter since this allows us to use one less attenuator and therefore costs marginally less.
5.1.3. Attenuator
Next high-level section: Receiver
An attenuator is a relatively simple circuit that produces an output power which is a desired fraction of the input power. Although I've used an IC for tighter tolerance and better frequency characteristics, the equivalent schematic is very simple and shown in Figure 13. There are several different resistor configurations to create an attenuator. The Pi attenuator shown below is just one of them.
We can get an even more complete picture if we explicitly show the source and load resistance. This is shown in Figure 14.
Typically, our source and load impedance will be matched to the characteristic impedance:
| (5.1.3.1) |
To find the attenuation, we need to find the voltage transfer function for the attenuator,
| (5.1.3.2a) | ||||
| (5.1.3.2b) | ||||
| (5.1.3.2c) | ||||
| (5.1.3.2d) | ||||
| (5.1.3.2e) |
Finally, we can rearrange our equations to represent the attenuator resistors in terms of the voltage transfer function,
| (5.1.3.3a) | ||||
| (5.1.3.3b) | ||||
| (5.1.3.3c) | ||||
| (5.1.3.3d) |
5.1.4. Directional Coupler
Next high-level section: Receiver
A coupler is a device that is able to share the power of a signal at an input port between two output ports. Its schematic depiction is shown in Figure 15.
The signal enters at the input port and most of the energy passes through to the transmitted port. Some input energy, however, exits through the coupled port where the amount is given by the coupling factor. See the relevent RF simulation section for more information on how this works. The insertion loss describes how much of the input power makes it to the transmitted port.
The equations for coupling factor and insertion loss are
| (5.1.4.1a) | ||||
| (5.1.4.1b) |
The coupler we use has a coupling factor of
Another important quantity for a coupler (it is often one of the most important criteria for assessing the quality of a coupler) is the coupler's directivity. It is given mathematically as
| (5.1.4.2) |
The directivity represents the ratio of the power available at the isolated port to the power available at the coupled port. Ideally, no power makes it to the isolated port, which would make the directivity infinite. Directivity permits the coupler to differentiate between forward and reverse signals. Having a high directivity is crucial for many devices (e.g. VNAs) but is less critical in our application. Indeed, the directional coupler used here was designed for simplicity of fabrication and to consume minimal board area, but exhibits poor directivity.
5.1.5. Power Amplifier
Next high-level section: Receiver
The power amplifier does exactly what its name suggests: it increases the signal power for transmission. This design uses a SE5004L power amplifier. The most important metrics for us to consider when choosing a power amplifier are the gain and
5.2. Receiver
A block diagram of the receiver is shown in 16. Its function is to capture the transmitted signal echo, amplify it without introducing too much noise, mix it with the transmitted signal down to an intermediate frequency, filter out non-signal frequencies and then amplify it again for digitization by the analog-to-digital converter (ADC). A simplified block diagram of the receiver hardware is shown below. Note that this is just one of two identical receivers. The mixer and differential amplifier support two separate differential signal pairs, so that circuitry is shared between both receivers.
5.2.1. Dynamic Range
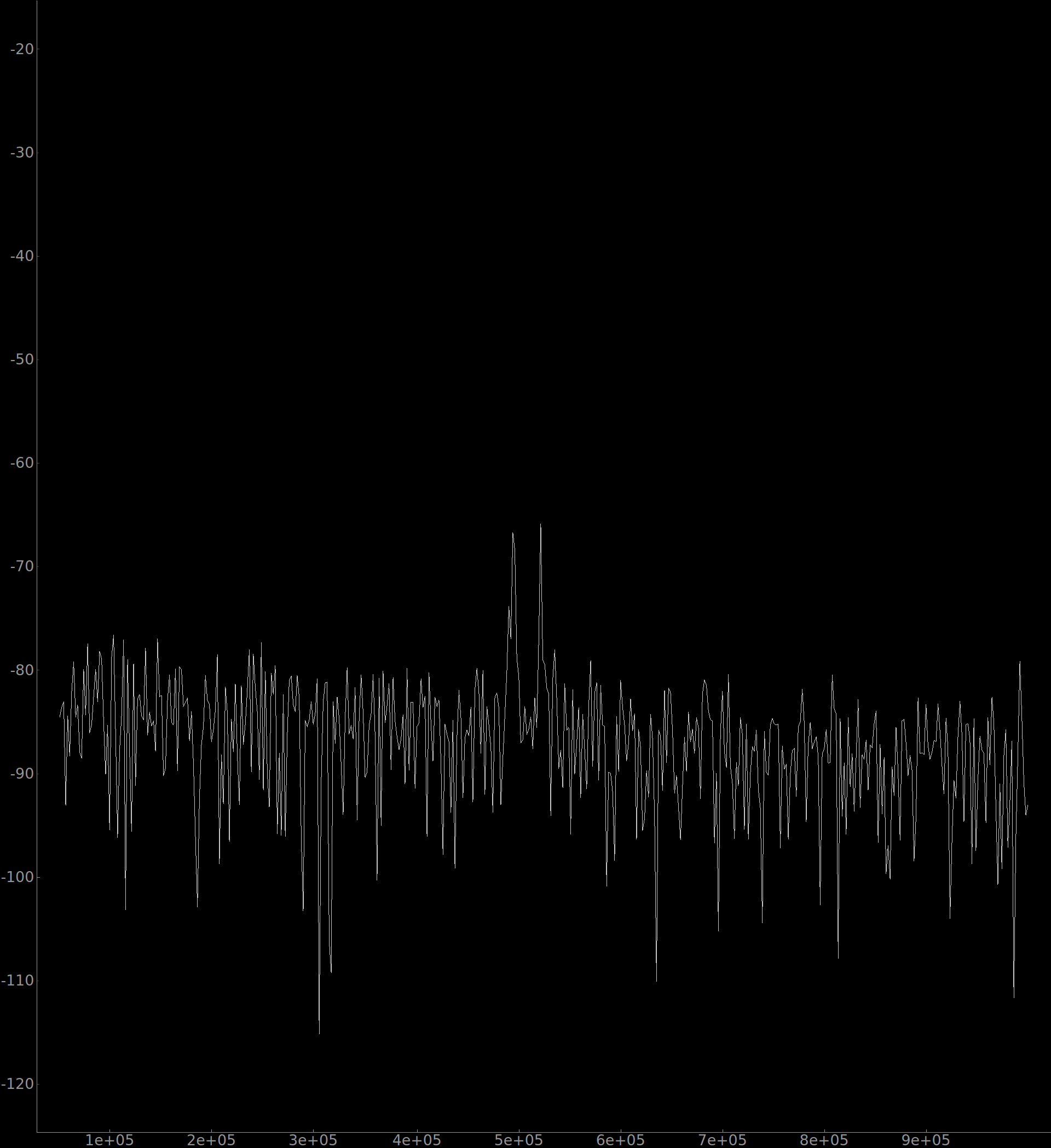
The radar's dynamic range is the ratio between the maximum signal the receiver can process and its noise floor. See those sections to see how the dynamic range was computed. We find that the theoretical dynamic range is equal to about
As discussed in the range section, the actual noise floor is higher than the theoretical value. A plot of the noise floor up to the decimated Nyquist frequency is shown in Figure 18.
5.2.1.1. Maximum Power
To find the maximum detectable power that avoids distortion, we can work backward from the ADC input voltage range of
| (5.2.1.1.1a) | ||||
| (5.2.1.1.1b) |
where
5.2.1.2. Minimum Power
Computing the minimum detectable power is more complicated than computing the maximum power. It requires first finding the voltage noise at the ADC input and then using the same procedure as in the maximum power section to relate this to an equivalent input power level.
We start by computing the thermal noise power at the reception antenna. This can be found with the equation
| (5.2.1.2.1) |
where
| (5.2.1.2.2a) | ||||
| (5.2.1.2.2b) |
The LNA and RF amplifier have their inputs and outputs matched to
| (5.2.1.2.3) |
where
Figure 20: Noise figure and gain of each receiver stage, along with the cumulative values.
So, adding
| (5.2.1.2.4) |
where
5.2.2. Mixer
Next high-level section: Differential Amplifier
A multiplicative mixer is a device that multiplies two input signals. Many mixers (including the one used in this design) are based on a Gilbert cell, whose schematic is shown in Figure 22.
The lower differential pair sets the gain of each of the top two differential pairs. For instance, if
To understand the operation, start by setting
If we set
| (5.2.2.1) |
where
5.2.3. Differential Amplifier
The differential amplifier's input circuitry is worth discussing because it affects the amplifier's frequency response. There are three logical parts to this, separated by dashed lines in Figure 23. The pullup resistors at the mixer output set the DC bias point of the output to
The frequency response of this circuit is shown in Figure 24.
5.2.3.1. Noise
Next high-level section: Digitization, Data Processing and USB Interface
The ADA4940 differential amplifier datasheet provides a method for estimating the output noise voltage given the feedback circuitry. Unlike the other receiver components, the differential amplifier is a relatively low-frequency component and does not have its ports matched to
To calculate the root-mean-square (RMS) output differential voltage noise density, the datasheet provides the equation
| (5.2.3.1.1) |
where
| (5.2.3.1.2a) | ||||
| (5.2.3.1.2b) | ||||
| (5.2.3.1.2c) | ||||
| (5.2.3.1.2d) | ||||
| (5.2.3.1.2e) | ||||
| (5.2.3.1.2f) | ||||
| (5.2.3.1.2g) | ||||
| (5.2.3.1.2h) | ||||
| (5.2.3.1.2i) | ||||
| (5.2.3.1.2j) | ||||
| (5.2.3.1.2k) | ||||
| (5.2.3.1.2l) | ||||
| (5.2.3.1.2m) | ||||
| (5.2.3.1.2n) | ||||
| (5.2.3.1.2o) | ||||
| (5.2.3.1.2p) | ||||
| (5.2.3.1.2q) |
Plugging all this in, we get
5.3. Digitization, Data Processing and USB Interface
An ADC converts differential analog signals from the receiver into 12-bit digital signals that are then sent to the FPGA for processing. The FPGA supports a two-way communication interface with the FT2232H USB interface chip that allows it to send processed data to the host PC for further processing and receive directions and a bitstream from the PC. A block diagram of this is shown in Figure 25. I've omitted the ADC's second input channel since it's identical to the first. Both channels are time-multiplexed across the same 12-bit data bus to the FPGA.
5.3.1. ADC
This design uses an LTC2292 ADC.
5.3.1.1. Input Filter
The ADC employs common-mode and differential-mode lowpass filters at its analog inputs (see Figure 25). The series resistors and outer capacitors serve as a lowpass filter for common-mode signals with a cutoff frequency of
5.3.1.2. Noise
The signal-to-noise ratio (SNR) of an ADC is equal to the ratio of the RMS value of a full-wave sinusoidal input (amplitude equal to the maximum input of the ADC) to the voltage noise RMS value. Mathematically,
| (5.3.1.2.1) |
The datasheet reports an SNR of
| (5.3.1.2.2a) | ||||
| (5.3.1.2.2b) |
5.3.2. FPGA
The heart of this project is its use of an FPGA, which offers unique performance attributes and design challenges. The FPGA serves two purposes: it performs data processing, and it acts as an interface to configure other ICs on the PCB. An FPGA can implement any digital logic circuit, within resource limitations, which gives us a tremendous amount of flexibility in regard to how we process the raw data and how to interact with and configure the other PCB ICs. The benefit of using the FPGA rather than software on the host PC for data processing is that it can run these algorithms faster than traditional software, and it also allows us to ease the burden on the USB data link between the radar and host PC. In regard to the second point, the bandwidth between the radar and host PC is limited by the USB 2.0 High Speed data transfer speeds of
This design uses an XC7A15T FPGA from Xilinx, which is a low-cost FPGA but is nonetheless sufficient for our needs. One additional benefit of using this FPGA is that it is pin-compatible with a number of higher resource count variants. Consequently, if our data processing needs expand in the future, we can use one of those variants as a drop-in replacement without otherwise altering the PCB.
5.3.2.1. Implementation
Next high-level section: FT2232H
The basic building block of an FPGA is a lookup table (LUT). Although LUTs can use any number of bits stored as a power of 2, these higher-level LUTs are all composed of a collection of simple 2-bit LUTs, shown in Figure 26.
The operation is very simple: to output the bit in the upper register we deassert the select line and to output the bit in the lower register we assert the select line. The register bits, called the bitmask, can be independently set.
We can already use this simple LUT to mimic the behavior of single-input logic gates. If we wanted the behavior of a buffer, we could write a 0 to bit 0 and a 1 to bit 1. The select line acts as the buffer input. A 0 here outputs a 0 and a 1 outputs a 1. To implement a NOT gate, we'd write a 1 to bit 0 and a 0 to bit 1.
It's instructive to double the size of the LUT to see how we can replicate two-input logic gates. A schematic for this is shown in Figure 27.
The select lines of the leftmost multiplexors are tied together to s0. The truth table for an AND gate is shown in Table 28. I've additionally included the bitmask number to show how the AND gate can be implemented.
Figure 28: Truth table for an AND gate, along with the necessary bit setting for an equivalent LUT.
So, the bitmask necessary to implement an AND gate is the bit in the out column for each bit number. In other words, bits 0 to 2 should be set to 0 and bit 3 should be set to 1. We can adjust this truth table for any other 2-input gate to show the correct bit mask to implement that gate.
Theoretically, we could now implement any combinational digital logic circuit with a sufficiently large interconnected array of these size-4 LUTs. Unfortunately, our processing circuit would be glacially slow. In particular, we haven't added any register elements (apart from the bit mask) so we wouldn't be able to pipeline our processing stream. Actual FPGAs incorporate LUTs and registers into larger structures often called logic blocks, which are designed to optimize pipeline performance for typical use cases.
FPGA implementations also need to address a number of other practical design challenges. Some of the most prominent of these are data storage, multiplication and clock generation and distribution. Although we can store processing data in the registers within logic blocks, we frequently need more storage than this provides. Additionally, using these registers for storage limits their use in pipelining, making the FPGA configuration slower and more difficult to route. To address this need, all but the simplest FPGAs come with dedicated RAM blocks.
Similarly, while LUTs can perform multiplication, they are needlessly inefficient in this regard. Since multiplication is highly critical in digital signal processing (DSP) applications, which is one of the major use cases for FPGAs, FPGAs have built-in hardware multipliers.
Finally, in regard to clocks, FPGAs often need to create derivative clock signals. This allows a portion of a design to be clocked at a much higher rate which correspondingly increases the throughput of the data processing stream. So, they are equipped with a number of phase-locked loops (PLLs). Additionally, it is critical that clock signals reach all registers with as little skew as possible. This makes timing closure (ensuring that all signals reach their destination register at the right time) much easier to achieve by the software tools that allocate FPGA resources. Because of this, FPGAs are built with dedicated, low-skew clock lines to all registers.
FPGAs are highly-complicated devices that require many sophisticated design considerations. This section mentioned only a few of the main ones.
5.3.3. FT2232H
The FT2232H is a USB interface chip that permits 2-way communication with the FPGA and enables us to load a bitstream onto the FPGA. The attached EEPROM chip is required to use the FT2232H in its FT245 synchronous FIFO mode, which allows the full
5.4. Power
The radar receives
Additionally, we have to pay special attention to the power supply rejection ratio (PSRR) of the linear regulators. Voltage regulators have high PSRR at low frequencies, but the PSRR typically falls off significantly as the frequency increases. Most of the buck converter noise occurs at its switching frequency, with additional noise at harmonics of this switching frequency (e.g.
Finally, of course, we need to make sure that the buck converters and linear regulators can supply enough output current for all downstream devices under full load.
5.4.1. Voltage Regulator Implementation
Next high-level section: FPGA Gateware
A simple implementation of a voltage regulator is shown in Figure 29. This has been adapted from AoE.
The operation of this circuit is very simple. The non-inverting input of the opamp is set by a current source supplying a zener diode. The current source provides a constant current over changes in the input voltage, so the voltage across the zener remains fixed at the desired reference. The inverting input is tied to a voltage divider output from the output voltage. The resistors are chosen to provide a desired output voltage for the reference voltage. Mathematically,
| (5.4.1.1) |
Finally, a darlington pair provides current amplification. So, for instance, even if our opamp could supply only about
It's important to consider
| (5.4.1.2) |
For large voltage drops and large currents, this can amount to a significant amount of power, which the transistor must be designed to handle. Moreover, this is wasted power, which is the reason for the use of LDO regulators in the radar.
It's also worth noting that this implementation has some drawbacks. For instance, it provides no current limiting and thus could be damaged if the output were shorted.
5.4.2. Voltage Converter Implementation
Next high-level section: FPGA Gateware
The operation of a voltage converter is more complicated than that of a voltage regulator. In this discussion we'll restrict ourselves to buck converters since that is what is used in the radar. That is, converters for which the output voltage is lower than the input voltage. However, the operation of boost converters and inverters is similar.
Figure 30 shows a possible implementation of a buck converter. This schematic has been adapted from AoE.
Ignore everything attached to the nMOS gate for the moment. We'll come back to it later. The salient point for now is that the transistor will be switched in a periodic way, with a percentage of that switching,
We can describe this circuit with two different equations: one when the transistor is switched on and one when it is off.
In the on state,
| (5.4.2.1a) | ||||
| (5.4.2.1b) | ||||
| (5.4.2.1c) | ||||
| (5.4.2.1d) |
And in the off state,
| (5.4.2.2a) | ||||
| (5.4.2.2b) | ||||
| (5.4.2.2c) | ||||
| (5.4.2.2d) | ||||
| (5.4.2.2e) |
To simplify the analysis, Eq. (5.4.2.2b) approximates
We can now impose the constraint
| (5.4.2.3) |
since otherwise the current would increase or decrease without bound. When we substitute in the current changes during the on and off states, we are left with following expression relating the input and output voltages:
| (5.4.2.4) |
Additionally, there are no lossy components here (aside from the small voltage drop between the nMOS drain and source) and so this device is theoretically 100% efficient. That is,
Before discussing the circuitry driving the transistor gate, it's worth addressing the Schottky diode which appears to play no role in the converter's function. Let's imagine what would happen if the diode were not present. When the transistor switches off, the inductor will go from seeing some current through it (call it
Now we can move on to the gate driver circuitry. The oscillator block produces two signals: a clock pulse and a sawtooth ramp with the same period and phase as the clock pulse. This is shown graphically in Figure 31.
Figure 31: Switching converter duty cycle control. Clock pulse (top) and sawtooth ramp (bottom).
The error amplifier outputs a voltage proportional to the difference between the reference voltage and the divided output voltage. The flip flop in this circuit is a set-reset (SR) flip flop. So, the instant a high voltage arrives at its set input the output will go high, and the instant a high voltage arrives at its reset input the output will go low. The output voltage will remain as the last value it was set as until another high set or reset changes its output. For example, even though the clock pulse drops low immediately after being asserted, the output remains high until the reset pin is asserted. So, when the clock pulse arrives, the output will go high and remain that way until the sawtooth ramps to a voltage higher than the error voltage.
To understand this better imagine what happens when the output voltage is higher than its target set by the feedback loop. In this case, the error amplifier decreases its voltage and the duty cycle of the nMOS is reduced. We determined above that
5.5. PCB layout
An image of the complete PCB layout is shown in Figure 32, with images of each layer shown in Figures 32, 33, 34, and 35.
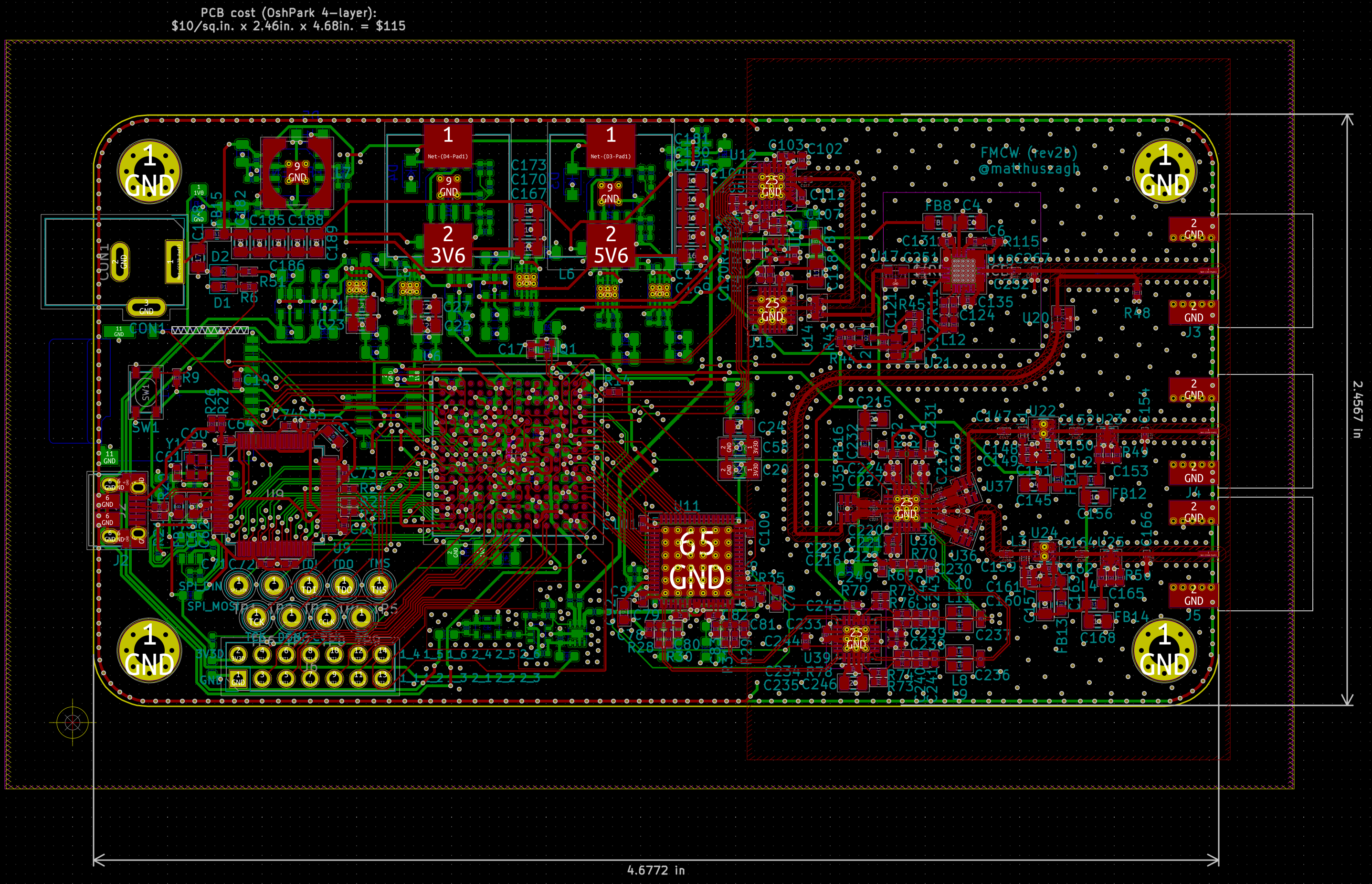
Figure 32: PCB layer 1. The top layer is a signal layer containing the sensitive RF circuitry on the right side and the digital circuitry on the left side.
Figure 35: PCB layer 4. The bottom layer is a signal layer and contains most of the power supply circuitry.
This is a 4-layer PCB in which the top and bottom layers are signal layers and the middle two layers are unbroken ground planes. The right portion of the top layer contains the transmitter and receiver, the left portion of the top layer contains mostly digital circuitry, and the bottom layer is primarily devoted to the power supply circuitry.
This separation of noise-sensitive RF circuitry from the digital circuitry is deliberate. Digital ICs tend to be noisy, and without proper separation, fast digital signals can inject noise into the receiver.
Despite physically separating the digital and analog circuitry, I've decided to use the same unbroken ground plane for each. The rationale for this is that the physical separation should be sufficient to prevent crosstalk from reaching the analog circuits. Moreover, separating the ground planes can create major issues if certain mistakes are made. In particular, there are a few digital signals that pass from the digital section into the analog section. Like all signal traces, these need low-inductance current return paths. When the ground planes are unbroken, the current can return on the ground plane directly adjacent to the relevent signal layer. When the ground planes are broken, the return current needs to find some other path to reach the source. This problem can be avoided by connecting the ground planes with a trace where the signal trace crosses the gap between the ground planes. When this return path is omitted, the fallback return path may have high inductance, creating voltage ringing and noise in the circuit. The additional isolation provided by separated ground planes is typically insignificant and therefore it's safer to keep the ground planes connected.
Another noteworthy decision is that I've used a ground plane on each internal layer, rather than a ground plane on one layer and a power plane on the other layer. Having a dedicated power plane can be useful when most of the PCB's circuitry is served by a single power plane. When this is the case, integrated circuits can receive power through a via between the power rail pin and power plane. This frees up routing space for signal traces. However, this radar requires a substantial number of power rails, which would either require a segmented power plane or a single continuous power plane that only supplies a few power pins leaving the remaining power pins to be supplied by traces. The first solution creates potential hazards when signal traces pass over gaps between individual power planes. The problem with this is identical to the problem raised by breaking up ground planes. Specifically, it can interrupt return currents and add noise to the PCB. The second solution provides us with essentially no benefit. Therefore, it makes more sense to just use an additional ground plane.
The third major decision I've made in regard to grounding is to use a ground fill (a ground plane filling the remaining space on a signal layer) around the sensitive RF circuitry, but not around the digital section on the left side of the top layer or around the power supply on the bottom layer. A ground fill, when used correctly with via fences and via stitching, can increase isolation between sensitive RF traces. A via fence is a series of tightly-spaced ground vias placed on either side of a trace, typically a transmission line. They act as a wall to fringing fields spreading from the transmission line and interfering with other traces or components. These are readily apparent around the microstrip transmission lines in Figure 32.
I've also added stitching vias in this section. Stitching vias are ground vias placed in a regular grid pattern to connect two or more ground regions. They provide a solid electrical (and thermal) connection between the ground fill and inner ground planes. These ensure that regions of the ground fill do not act like unintentional antennas. The general rule-of-thumb for via fences and stitching vias is to place them at a separation of
I've omitted the ground fill in other regions because of this unintended antenna effect. The improved isolation between traces is important in the sensitive RF section, but is less critical in the digital and power supply regions. Moreover, these regions have a higher density of traces, which would cause a ground fill here to be broken up more. This increases the chance of leaving an unconnected island of copper that could act as an antenna and increase noise in the resulting circuit.
Decoupling (or bypass) capacitor placement is another important consideration for reducing circuit noise. Decoupling capacitors are typically placed adjacent to IC's on a PCB. They serve essentially 2 purposes, which are thematically different but physically the same. The first purpose is that they provide a low-impedance supply of charge to the integrated circuit. This is especially important with digital ICs which draw most of their current during a periodic and small fraction of their clock duty cycle. These are called current transients and the decoupling capacitor acts as the supply of charge for these sudden rises in current draw. Power supplies are unable to satisfy these sudden current demands since they take time to adjust to their current output.
The 2nd reason (which is actually equivalent) is that they prevent noise from leaving the IC and reentering the power supply. The noise is caused by these sudden changes in current. The decoupling capacitors provide a low impedance path for this noise to ground. Analog circuits also require decoupling capacitors, primarily to further isolate themselves from the noise of digital circuits.
Decoupling capacitors can be delineated into 2 size gradations. The first and most important variety are the small (size and value) decoupling capacitors placed immediately adjacent to the ICs whose power supply they decouple. Since these capacitors come in small packages they have low inductance values (inductance is the most critical impedance factor at high frequencies) and therefore are able to provide the current needs for very fast transients. The fact that they are relatively low in value is due to the fact that it's more expensive to put a large capacitance value in a small package. Otherwise, you want the largest capacitance value for the size. The ideal capacitor for this purpose is typically a
In regard to layout, the small decoupling capacitors should be placed in a way that minimizes the inductance between the power supply and ground pins. Where possible, I've placed the decoupling capacitor immediately next to the IC it serves with direct, short connections to the power and ground pins. In cases where this would block a signal trace, I've placed the bypass capacitor as close to the pins it serves as possible and placed two vias to the ground plane: one at the ground pin of the IC and another at the ground side of the capacitor. For ball grid array (BGA) packages (just the FPGA in this design), it's not possible to place bypass capacitors on the same side as the component and next to the pins they serve. In this case, I've placed the bypass capacitors on the other side of the PCB directly below the component, with vias connecting the capacitor and component pins.
There are a few other design decisions worth mentioning. The first is that I've placed ground vias adjacent to all signal vias. This allows the return current to easily jump between the inner ground planes when a signal moves between the top and bottom layers. Additionally, I've added a perimeter ground trace with a via fence. The copper planes of a PCB can cause the inner substrate layers to act as a waveguide for radiation originating at signal vias. This ground perimeter acts as a wall, preventing radiation from leaving or entering the PCB.
6. FPGA Gateware
As noted, the FPGA in this radar performs real-time processing of signal frequency differences to calculate the distance of detected objects without resulting in any noticeable latency. Additionally, it provides a state machine for interacting with the radar from a host PC and configures other ICs on the PCB. This section and its subsections contain a number of block diagrams and associated descriptions. These diagrams provide a functional description of the operations performed by the Verilog code I wrote.
This FPGA code supplements the functionality of Henrik's VHDL FPGA code, which enabled host PC interaction with the radar and filtering, by including a window function and FFT, and by allowing the transmission of data from any intermediate processing step to the host PC in real time. This means that we can view the raw data, post-filter data, post-window data or fully-processed post-FFT data. All of this can be specified in software with immediate effect (i.e., without recompiling the FPGA code). This enhanced functionality and flexibility required rewriting all of the FPGA code from scratch. It also required more sophisticated temporary data storage, implemented as synchronous and asynchronous FIFOs (first-in first-out buffers) with associated control logic. In particular, the ability to retrieve a full raw sweep of data (20480 samples of 12 bits), while also being able to configure the FPGA to send data from any other processing step required efficient use of the limited memory resources on the FPGA. Finally, Henrik's implementation uses an FIR core provided by Xilinx. I've created my own implementation, which makes it easier to simulate the design as a whole and allows using tools other than Vivado (e.g., yosys, if/when it fully supports Xilinx 7-series FPGAs).
A top-level block diagram of the FPGA logic is shown in Figure 36. The data output by the ADC (see receiver) enters the FPGA and is demultiplexed into channels A and B, corresponding to the two receivers. For a simple range detection (i.e., ignoring incident angle), one channel is dropped (like most things, channel selection is configurable at runtime in the interfacing software). The selected channel is input to a polyphase FIR decimation filter that filters out frequencies above
When the bitstream is fully loaded onto the FPGA, the FPGA control logic waits for ADF4158 configuration data from the host PC software. It also requires several other pieces of information from the host PC, such as the receiver channel to use and the desired output (raw data, post-FIR, post-window, or post-FFT). Once the FPGA receives a start signal from the host PC, it configures the frequency synthesizer and then immediately begins capturing and processing data. The data processing action is synchronized to a muxout signal from the frequency synthesizer indicating when the frequency ramp is active. The FPGA waits until all transmission data has successfully been sent to the host PC before attempting to capture and process another sweep. This ensures that the host PC always gets full sweeps. This process is repeated until the host PC sends a stop signal, at which point the FPGA is brought into an idle state, waiting to be reconfigured and restarted.
6.1. FIR Polyphase Decimation Filter
The FIR polyphase decimation filter has two functions: it filters out signals above
We can't downsample before filtering because that would alias signals above
The filter's frequency response is shown in Figure 37. It was designed using the remez function from SciPy.
Figure 37: FIR frequency response from DC to
The stopband, which stretches from
6.1.1. Implementation
Next high-level section: Kaiser Window
In order for our polyphase decimation FIR filter to work it needs to produce results identical to what we'd get if we first filtered our signal and then downsampled. Our input signal arrives at
Start with the normal equation for an FIR filter:
| (6.1.1.1) |
| (6.1.1.2a) | ||||
| (6.1.1.2b) | ||||
| (6.1.1.2c) | ||||
| (6.1.1.2d) | ||||
| (6.1.1.2e) | ||||
| (6.1.1.2f) | ||||
None of this is different than a normal FIR filter so far. The difference comes in noticing that the only results we want after filtering and downsampling are
| (6.1.1.3a) | ||||
| (6.1.1.3b) | ||||
| (6.1.1.3c) | ||||
| (6.1.1.3d) | ||||
| (6.1.1.3e) | ||||
And these should arrive at the output at a frequency of
We need to figure out how to compute this directly, i.e., without filtering and then downsampling as we did above. Figure 38 implements this.
The leftmost (vertically stacked) flip-flops make up a shift register clocked at
You may have noticed that if we followed this diagram precisely, we would need 120 multiplication blocks. That's significantly more than the 45 digital signal processing (DSP) slices we get on our XC7A15T FPGA. Luckily, we can deviate from the diagram and use our multiplies much more efficiently. The key to this is that DSP slices can be clocked at a much higher frequency (typically several hundred MHz) than the frequency at which we're using them (
By using the multiplies more efficiently, the number of DSP elements is no longer the resource-limiting factor. Instead, we're limited by the number of flip-flops needed for the filter banks. In the current implementation we have 120 filter bank memory elements that must each store 12 bits, which means 1440 flip-flops. We have room to increase this, but a 120-tap filter should be good enough. We could potentially cut down on resources by replacing the filter bank flip-flops with time-multiplexed block RAM (BRAM) in much the same way as the DSP slices. However, this is not a trivial task. Each bank only needs to hold 72 bits, but the minimum size of a BRAM element is 18kb. So, the simple implementation of using one BRAM per bank would waste a lot of storage space. Other modules, such as the FFT and various FIFOs need this limited RAM and use it much more efficiently; we only have a total of 50 18kb RAM blocks. We could try to be a bit more clever and share a single BRAM across multiple banks. But, this would require additional control circuitry and would complicate the module somewhat. If we end up needing a better FIR module, this could be worth investigating, but for the time being our FIR is good enough.
6.2. Kaiser Window
Windowing is used to reduce spectral leakage in our input signal before performing an FFT on that signal. The following subsections describe what spectral leakage is, how windowing helps to reduce it, and how to implement a window function on an FPGA.
6.2.1. Spectral Leakage
Next high-level section: FFT
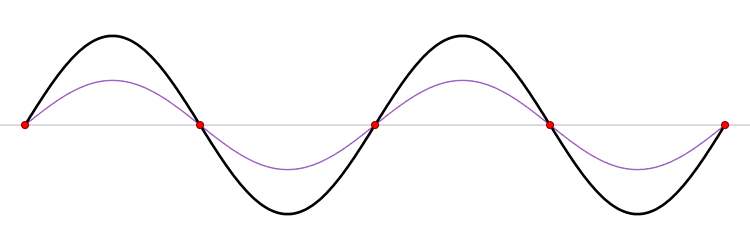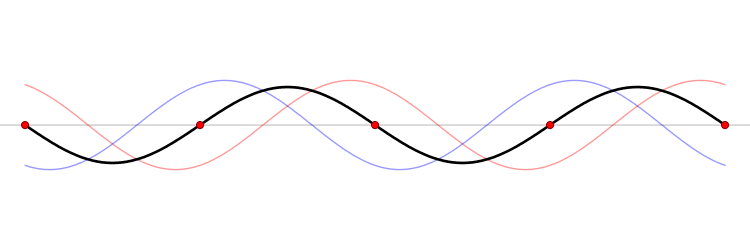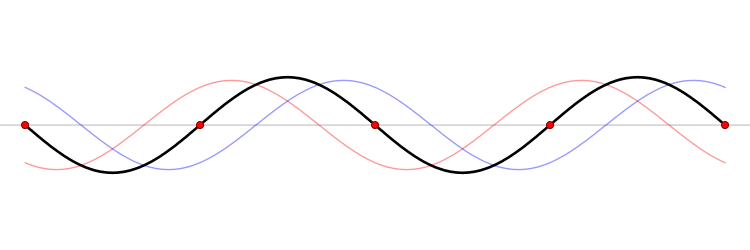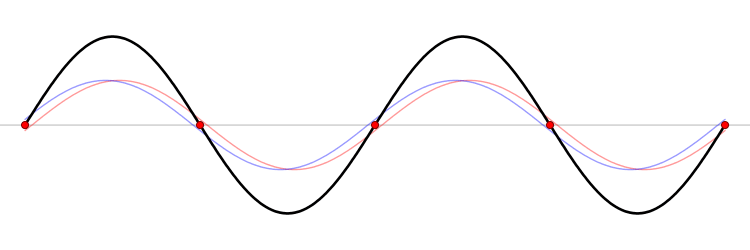
Spectral leakage occurs when an operation introduces frequencies into a signal that were not present in the original signal. In our case, spectral leakage is due to an implicit rectangular window performed on our input by taking a finite-duration subsample of the original signal. The plots in Figure 39 illustrate this effect for a single-frequency sinusoidal input.
We see that the beginning and end of the sample sequence jump from zero to some nonzero value. This corresponds to high frequency components that are not present in the original signal, but that we can detect in the FFT output. We could eliminate the spectral leakage by windowing an exact integral number of periods of the input signal. But we can't rely on being able to do this, especially for signals composed of multiple frequencies.
Some examples of sample sequences illustrate the various effects spectral leakage can have.
Start with a simple sinusoid with frequency 1Hz. We'll always ensure the sampling rate is at or above the Nyquist rate to avoid aliasing.
In Figure 40, the first plot below shows the input sample sequence and the interpolated sine wave. The second shows the resulting FFT.
If the FFT correctly represented the true input signal, the entire spectral content would be within the 0.94Hz frequency bin. The fact that it also registers spectral content at other frequencies reflects the spectral leakage.
If we change the phase of the input signal, the output will change as well, which shows the dependence of our output on uncontrolled variations in the input. This effect is illustrated in Figure 41.
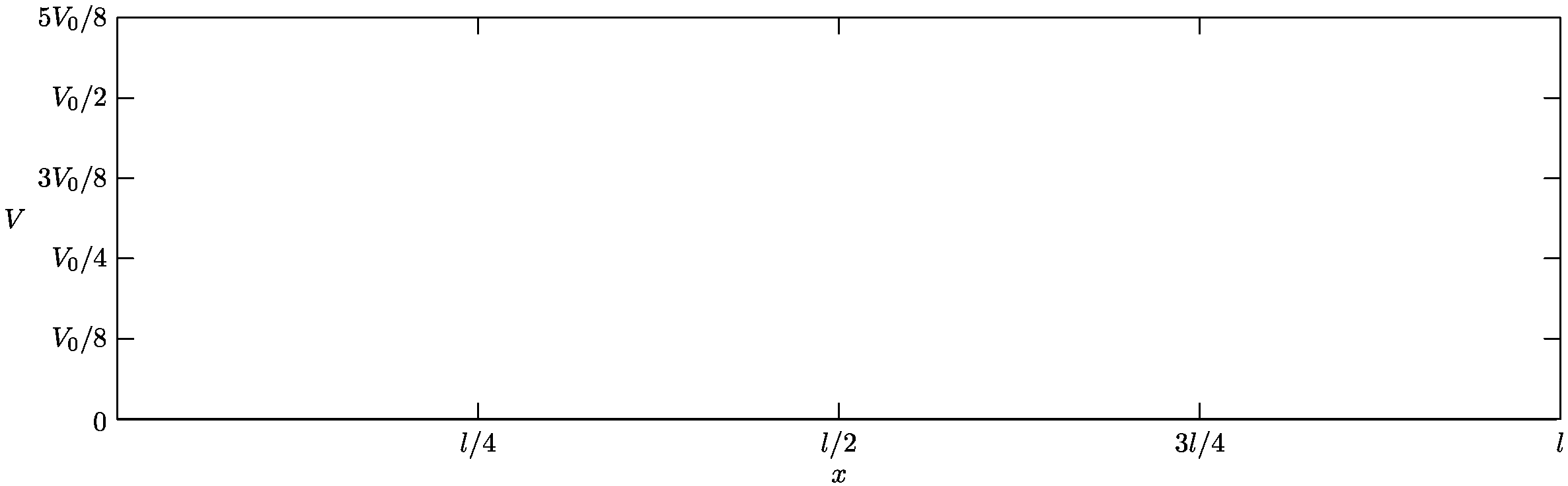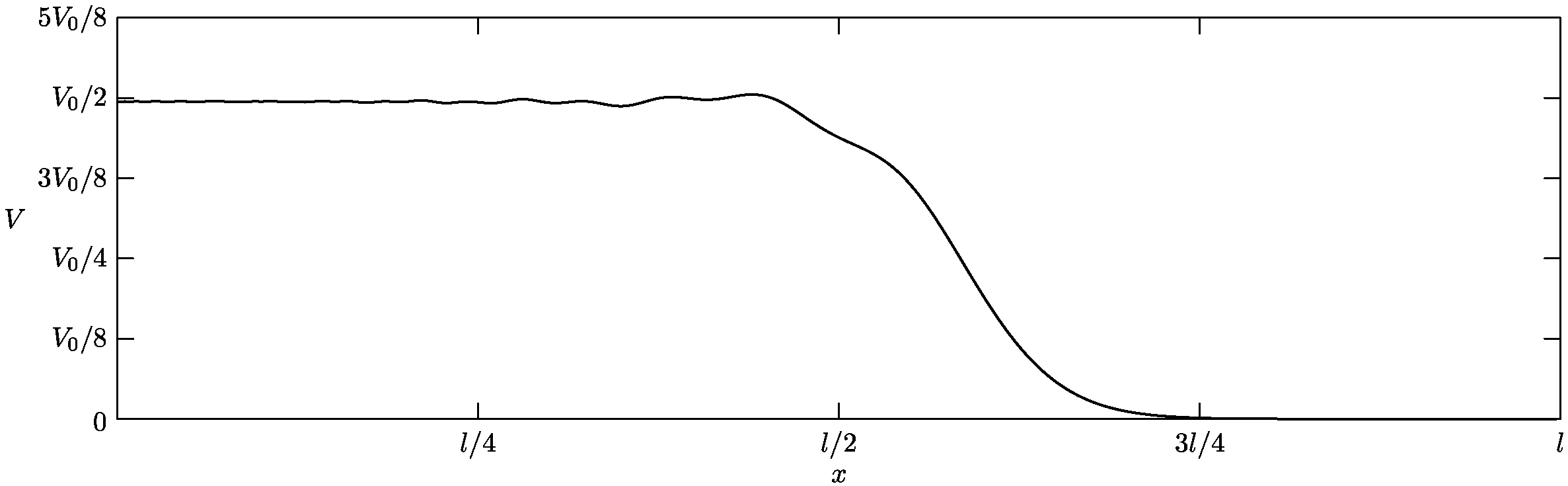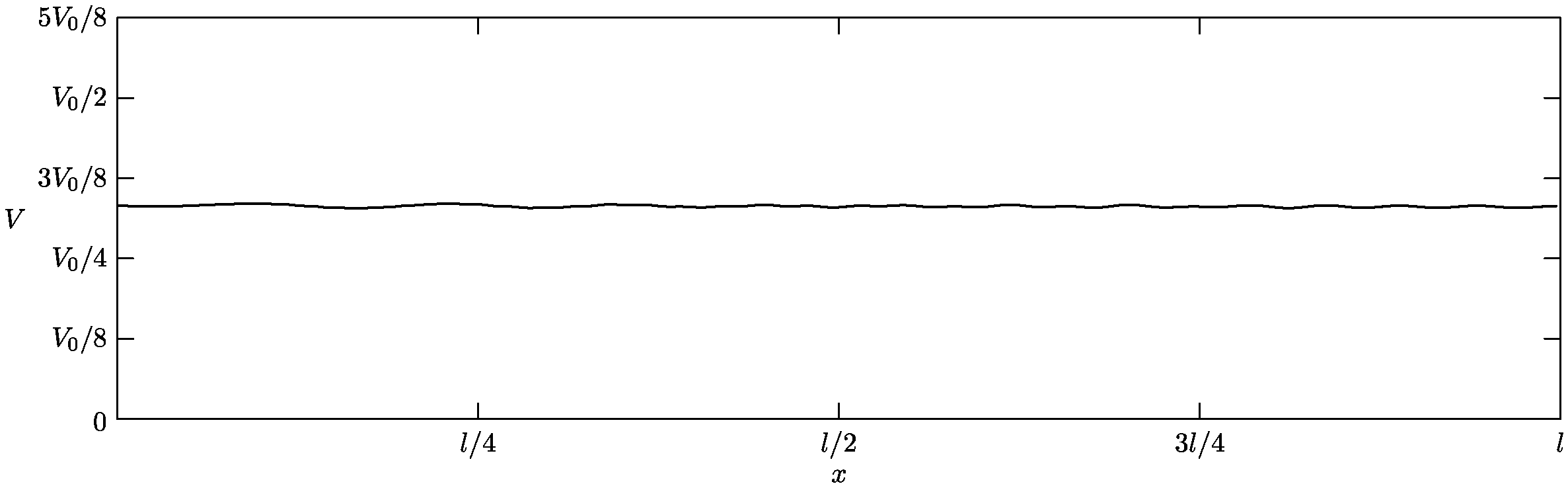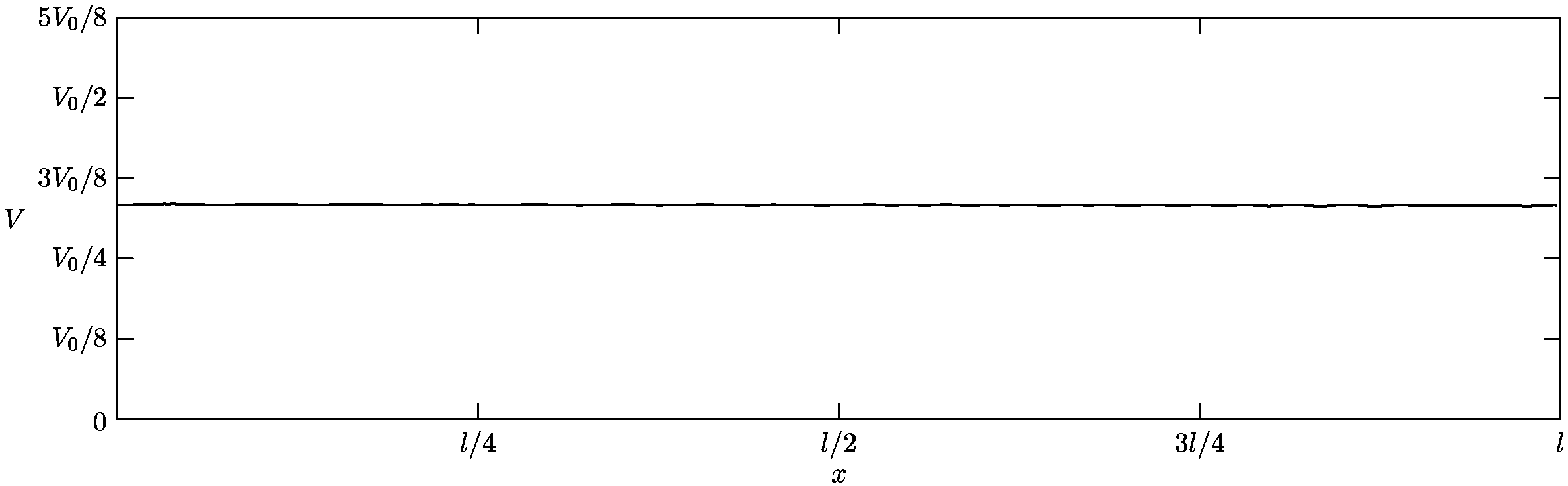
Figure 42 shows the effect of using a larger FFT on the spectral leakage. Namely, the leakage still exists, but is less pronounced. This is expected because the distortion produced at the beginning and end of the sampled signal now account for a smaller proportion of the total measured sequence.
6.2.2. Effect of Windowing on Spectral Leakage
Windowing functions can be effective at reducing spectral leakage. Figure 43 shows the effect of performing a kaiser window function on a sampled sequence before computing its spectrum.
For the windowed function, the spectral content outside the immediate vicinity of the signal frequency is almost zero. To understand how the window works, it is informative to compare the original time-domain signal with the time-domain signal with windowing. A plot of this is shown in Figure 44.
We see that the kaiser window works by reducing the strength of the signal at the beginning and end of the sequence. This makes sense, since it is these parts of the sample that create the discontinuities and generate frequencies not present in the original signal.
6.2.3. Implementation
A window function works by simply multiplying the input signal by the window coefficients. Therefore, implementing one on an FPGA is very easy. We can use numpy to generate the coefficients for us, write these values in hexadecimal format to a file, and load them into an FPGA ROM with readmemh. See the window module for details.
6.3. FFT
An FFT is a computationally-efficient implementation of a discrete fourier transform (DFT), which decomposes a discretized, time-domain signal into its frequency spectrum. The frequency is related to the remote object distance, so it's a short step from the frequency data to the final, processed distance data.
6.3.1. Implementation
Next high level section: Additional Considerations
There are several important considerations when implementing an FFT in hardware. First, it should be pipelined in a way that allows a high clock rate and bandwidth. Additionally, it should use as few physical resources as possible, which for an FFT involves the number of multipliers, adders, and memory size. I spent some time looking through relevant research papers to find a resource-efficient algorithm that would fit on a low-cost FPGA, and settled on the R2²SDF algorithm2, which requires that
Figure 45 shows a block diagram of the hardware implementation, adapted from the original paper.
The N blocks above the BF blocks denote shift registers of the indicated size. The BF blocks denote the butterfly stages with multipliers between each successive stage. The data comes streaming out on the right side in bit-reversed order. This structure is shown in significantly more detail in Figure 46, which shows just the last 2 stages and omits the select line control logic to save space (see the Verilog file for full details).
A few things are worth noting here. Each shift register requires only 1 read and 1 write port (we only write the first value and read the last value each clock period) and therefore can be implemented using dual-port BRAM (see the shift_reg module for the actual implementation). Since the RAM module is described behaviorally, the synthesis tool can decide when it makes sense to use BRAM instead of discrete registers (see the fft_bfi and fft_bfii files). I've also added a register after the complex multiplier to show how this can be pipelined, but the actual module uses more pipeline stages. Lastly, the multiplier in the diagram is a complex multiplier, meaning that it requires 4 real multiplication operations. However, it's possible to use 3 DSP slices for this. Or, if we were really determined, just 1. The current implementation uses 3, although a previous implementation used 1 successfully. The challenge with using just 1 DSP is that it requires additional considerations to meet timing. To understand how we can turn 4 DSP slices into 3, we must consider a complex multiplication:
| (6.3.1.1) |
where
| (6.3.1.2a) | ||||
| (6.3.1.2b) |
the result can be achieved with
| (6.3.1.3a) | ||||
| (6.3.1.3b) |
If we wanted to, we could also cut down on the number of additions used since
Lastly, I'll discuss the initial steps for how we could turn the 3 DSP slices into 1, even though I haven't used it in my implementation. I've chosen to discuss it because I've used the same strategy elsewhere in the FPGA code, and it might be necessary in the future if we add functionality that requires further DSP usage.
The key principle, like with the FIR filter, is that we can run our DSP slice much faster than the general FFT clock rate of
Figure 47: Phase counter timing diagram.
Clearly, the distinguishing factor when both clocks are at their rising edge is that the
reg clk40_last; reg [1:0] ctr; always @(posedge clk120) begin clk40_last <= clk40; if (~clk40_last & clk40) begin ctr <= 2'd1; end else begin if (ctr == 2'd2) begin ctr <= 2'd0; end else begin ctr <= ctr + 1'b1; end end end
But it's a bad idea to use a clock in combinational logic as we've done here. The reason is that FPGA vendors provide dedicated routing paths for clock signals in order to minimize skew and make timing requirements easier to meet. By using clocks in combinational circuits we run the risk of preventing the router from using these dedicated paths. Instead, it would be great if we could use a dual-edge triggered flip flop that used both
module dual_ff ( input wire clk, input wire rst_n, input wire dp, input wire dn, output wire q ); reg p, n; always @(posedge clk) begin if (~rst_n) p <= 1'b0; else p <= dp ^ n; end always @(negedge clk) begin if (~rst_n) n <= 1'b0; else n <= dn ^ p; end assign q = p ^ n; endmodule
The ^ denotes an exclusive-or (xor) operation. This module takes advantage of the fact that a binary value xor'd by the same value twice just gives the original value. To understand how this works, imagine the positive clock edge occurs first. The flip-flop state at that edge will be (dp^n)^n. xor is an associative property so this is equal to dp^(n^n). n^n must be 0 and dp^0 is just dp. For the negative edge, the output is p^dn^p. xor is also commutative, so this is p^p^dn, which is of course dn. It's now easy to adjust our counter module to keep the clock out of combinational logic. For the full details see the pll_sync_ctr and dual_ff modules.
6.4. Asynchronous FIFO
A FIFO, or first-in first-out buffer, is a type of temporary data storage. It is characterized by the fact that a read retrieves the oldest item from the buffer. Additionally, reads and writes can be performed simultaneously. There are essentially two different types of FIFOs: synchronous and asynchronous. In a synchronous FIFO, the read and write ports belong to the same clock domain (a clock domain is a group of flip-flops synchronized by clock signals with a fixed phase relationship). In an asynchronous FIFO, the read and write ports belong to different clock domains. Therefore, asynchronous FIFOs are useful when sending data between clock domains. In this radar, I've used synchronous FIFOs to temporarily store the output of data processing modules before passing that data to other modules for further processing. I've used asynchronous FIFOs to handle the bidirectional communication between the FT2232H USB interface IC and the FPGA, which are synchronized by independent clocks.
6.4.1. Implementation
Next high level section: Additional Considerations
In contrast to synchronous FIFOs, which are simple to implement, asynchronous FIFOs present a few design challenges related to clock domain crossing. The ideas in this section come from an excellent paper on asynchronous FIFO design by Clifford Cummings.3
When implementing a synchronous FIFO, we can keep track of whether the FIFO is empty or full by using a counter. The counter is incremented when a write occurs and decremented when a read occurs. The FIFO is empty when the counter value is 0 and full when it reaches a value equal to the size of the underlying storage.
An asynchronous FIFO cannot use the counter method, since the counter would need to be clocked by two asynchronous clocks. Instead, the asynchronous FIFO needs to keep track of a read address in the read clock domain and a write address in the write clock domain. There are three primary difficulties that an asynchronous FIFO implementation must address. The first is that we need to somehow use the read and write addresses to determine when the FIFO is empty or full. The second is that in order to compare these addresses, they need to cross into the other's clock domain. The third difficulty is that a reset will necessarily be asynchronous in at least one of the clock domains. Let's address these concerns one-by-one, starting with the full and empty conditions. Moreover, we'll initially ignore the fact that the read and write pointers must cross a clock domain.
Imagine the size-8 memory storage device shown in Figure 48. At initialization or reset, the read and write pointers both point to address zero. The pointers always point to the next address to be written or read. When a new word is written to the FIFO, the write is performed and then the write address is incremented to point to the next address.
Figure 48: FIFO read and write address at reset.
Clearly, at reset the FIFO is empty since we haven't yet written anything into the FIFO. So, we can signal the empty flag when the read and write addresses are the same.
To fill the FIFO, we write 8 words without reading. However, now the write address points again to address 0. So the full flag is signaled also by the write address and the read address being the same as shown in Figure 49.
Figure 49: FIFO empty condition.
This is of course a problem. We can solve this by using an extra bit to denote the read and write pointers, as shown in Figure 50. Now, at reset the read address will have the value 0000 and the write address will have the same value. When the write pointer increments back to address 0, it will have the value 1000.
Figure 50: FIFO full condition.
If our read address then catches up to the write address, it will also have the value 1000. So, we have a clear way to distinguish our empty and full conditions. Namely, the FIFO is empty when all read address bits are the same as all write address bits, and the FIFO is full when all bits except for the MSB are the same.
Now, let's address the difficulty that the read address must cross into the write clock domain in order to check for a full condition and the write address must cross into the read clock domain in order to check for an empty condition. To perform these clock domain crossings, we can use a 2 flip-flop synchronizer.
A flip-flop synchronizer is a simple device that passes a signal through a series of flip-flops (typically, 2) in the destination clock domain in order to reduce the probability that a metastable state propagates to downstream logic, which could cause state machines to enter into undefined states and create unpredictable circuit behavior. When the setup or hold times of a flip-flop are violated the flip-flop's output can go metastable, which means that it is temporarily at a value between its high and low states. The duration of this metastable state can be short or quite long. When the metastable state lasts sufficiently long, it can be registered by the next flip-flop, creating a chain reaction. A flip-flop synchronizer works by placing a few flip-flops as close together as possible, so as to minimize the signal propagation delay between the flip-flops. The proximity is important because it maximizes the amount of time a flip-flop can be in a metastable state and still pass a definite state to the next flip-flop. Using two flip-flop synchronizers instead of one decreases the likelihood that we pass the metastable state on to the downstream circuitry. We can think about this in terms of the probability,
By using a flip-flop synchronizer to pass the read address into the write domain and the write address into the read domain, we are comparing a potentially old read address with the current write address and a potentially old write address with the current read address. This raises the question of whether this delay creates the possibility of underflow (performing a read when the FIFO is empty) or overflow (performing a write when the FIFO is full). The answer to this question is that there is no risk of underflow or overflow, and the reason is intuitive. When we're checking the full condition, the write address is correct and the read address is potentially a little old. This means that, in the worst case, we measure the buffer as being slightly more full than it is in reality. When we check the empty condition, we might measure the buffer as being slightly more empty than it actually is, but never more full.
There's still a problem we haven't addressed though. The current implementation has us sending binary counters across domains. Binary counters have the unfortunate attribute that incrementing a value by 1 can result in all of the value's bits changing. Since all counter bits will generally not change simultaneously, the output value in the new domain has a reasonable chance of taking on any address value. Instead of using binary counters we can use Gray codes, which avoid this problem. Successive increments (or decrements) in a Gray code differ by exactly one bit, which means that we will either register the old or new state, and not some random state. To understand the difference between binary and Gray codes, Table 51 shows the decimal numbers 0 through 7 and the corresponding binary and Gray codes.
Figure 51: Decimal numbers 0 to 7 and the corresponding binary and Gray codes.
Binary counters are still useful in this context because they are used to address the underlying block RAM and make it easy to perform an increment operation. So, the read address in the read domain and write address in the write domain can be stored and updated as binary codes, but converted into Gray codes for comparison. Fortunately, converting a binary code into a Gray code is simple. If WIDTH is the bit width of the binary and Gray codes, bin is the binary code and gray is the Gray code, then the following Verilog code performs the conversion.
wire [WIDTH-1:0] gray = (bin >> 1) ^ bin;
The final challenge we need to address in the asynchronous FIFO implementation deals with resetting the FIFO. The reset is necessary to start the FIFO in a known, initialized state as well as to perform any resets needed during runtime. The difficulty with implementing the reset comes from the fact that a synchronous reset in the write clock domain is asynchronous in the read clock domain. Similarly, a synchronous reset in the read clock domain is asynchronous in the write clock domain. So, we're forced to use some sort of asynchronous reset here. There are a number of different ways the reset can be performed, including using a synchronous reset in the write domain that is asynchronous in the read domain. This has the advantage of allowing writes to recommence sooner after the reset is asserted since we don't need to synchronize exiting the reset. Since this additional performance isn't critical in our application, I've chosen to make the reset asynchronous in both domains, thus allowing it to be triggered from either domain. This reset is then synchronized into both domains. A reset in the read domain causes the empty flag to be asserted and the read address to be reset and a reset in the write domain causes the full flag to be asserted and the write address to be reset. If the read reset deasserts first, the empty flag will remain asserted because the read and write addresses are identical. If the write reset deasserts first, then the full flag will deassert and we can begin writing to the FIFO.
6.5. Additional Considerations
6.5.1. Convergent Rounding
When performing computations on an FPGA we're often faced with representing real numbers using a small number of bits. Specifically, we must do this with real numbers where the fractional value is a large percentage of the total value so we can't simply ignore the non-integral part. CPUs and numerical software use floating point arithmetic to achieve good precision for a wide dynamic range of values. The trick is that successive intervals between numbers are non-constant. The intervals between small numbers are small and the intervals between large numbers large. In other words, the focus is on minimizing the percentage error, not the total error, while allowing a very large range. FPGAs will sometimes implement floating point. However, compared to integer arithmetic, floating point arithmetic is very resource intensive on an FPGA, so this is only done when the design has a strict accuracy requirement and the much higher FPGA cost is worth it.
Twos complement provides us with a good way to represent integral values but doesn't directly give us a way to represent real numbers. However, the way to extend it for this need is simple: we can sacrifice range for precision. For instance, imagine we represent a number with 10 bits. Twos complement would give us a range of -512 to +511. But imagine that our range of values is between -1 and +1. If we multiply all of our real values by
We might do this to multiply an integral value by a fractional value and get the approximately integral result. The problem is that we're implicitly rounding the result in the last step (right bit shift). And, we're using a bad method of rounding: truncation. This might be fine if the result is final. However, if we then use the result in subsequent truncations the bias that we introduce in each truncation can build up and develop a significant bias in the final result. A good solution is to use something called convergent rounding. The zipcpu blog provides an excellent description of this as well as additional rounding methods and their merits. The diagram below is adapted from that post. I'll skip the alternative methods and just discuss convergent rounding.
The basic idea of convergent rounding is to round most numbers toward their nearest integral value, and to round numbers equidistant between two integers to the nearest even integer. This is shown diagrammatically in Figure 52. The numbers in parantheses represent the actual values and the numbers outside the parentheses shows its representation in terms of how it would be interpreted as a traditional twos complement value. Clearly, the mapping between numbers represents a bit shift of 3. The colors show the final mapped value (i.e. all green values get a final value of 0, etc.) and the boxes with thick boundaries show values equidistant between two final values.
We can see that the rounding behavior is symmetric about
Here's the combinational Verilog code to achieve this. OW represents the output bit width, IW represents the input bit width and indata is the input data. post_trunc, of course, is the final, rounded result.
assign pre_trunc = indata + {{OW{1'b0}}, indata[IW-OW], {IW-OW-1{!indata[IW-OW]}}}; assign post_trunc = pre_trunc[IW-1:IW-OW];
It's helpful to think about actual bit widths to see what's going on here. Take an input width of 7 and output width of 3. The Verilog code above performs the addition
Figure 53: Bracketed values represent an input data bit position. Non-bracketed values denote a literal bit value. The vertical line shows the radix point position.
post_trunc will be the result to the left of the radix point after the addition is performed. To understand how this works, start with positive numbers (i.e. bit 6 is 0). A bit 4 value of 1 means the integral part is odd, and 0 corresponds to an even integral part. If bit 3 is 1 the fractional part has a value of at least 0.5. If the input integral part is odd and has a fractional part of 0.5, we get a carry bit from bit position 3 and our value rounds up to the next higher integer. If the integral part is even we don't get a carry bit and we round down. If we have a fractional part other than 0.5, bits 0-2 ensure we get the normal nearest-integer rounding. For instance, if we have an even integral value and fractional part greater than 0.5 the inverted bit 4s will give us a carry bit and we'll round up. It's not hard to follow this trend to see we get the correct behavior in the other cases.
For negative values, a 1 (0) in bit 4 means an even (odd) integral part. This flips the rounding behavior on the boundary. For instance, an even integral part will round up (effectively truncating the integer) and an odd integral part will round down.
6.5.2. Formal Verification and Testing
A number of Verilog modules use Symbiyosys for formal verification. Currently, only a small portion of the design is formally verified. In this context, it is used primarily as an additional form of testing. See the code for details. All formal verification tests can be run from the Verilog directory Makefile with make formal.
I've used Cocotb for creating and running automated test benches. Again, see the code for details. All tests can be run from the Verilog directory Makefile with make test.
7. PC Software
The host PC software has several important tasks. First, it must provide the user with a shell environment to query the current FPGA configuration, write a new configuration, and set various plotting and logging options. Setting the FPGA configuration requires being able to write data to the FTDI FT2232H device.
Next, it must extract each sweep from the raw bytes sent from the FPGA. This needs to be performed efficiently, otherwise it can act as a serious bottleneck. I initially implemented this code entirely in Python but was only able to receive about 10 sweeps per second. Conversely, by rewriting this same code in C (incorporated into the Python code with Cython) I'm able to receive several hundred sweeps each second.
Depending on the user-requested configuration, the software must also perform some data processing. The FPGA gateware and host PC software have been setup so that any intermediate data (raw ADC, FIR downsampled, window, or FFT) can be sent from the FPGA to the PC. Additionally, any final output data can be requested for viewing. For instance, the user might request raw data from the FPGA and FFT data as the final output, which would require the software to perform the polyphase FIR filter, the kaiser window and the FFT. This is, of course, fairly straightforward with numpy and scipy.
The last main task performed by the PC software is plotting. I'm using PyQtGraph, which is excellent for real-time plotting. The user can choose to plot the data as a time-series (except FFT output), as a frequency spectrum, or as a 2D histogram displaying the frequency spectrum over time. If a non-FFT final output is requested for the spectrum or histogram plot, an FFT of the time-series data is taken before plotting.
All of these options (with the exception of the time-series plot) work in real time. In fact, the time-series plot could be made to work in real time by decreasing the plot update rate, but this would make it too fast to see.
The C source code that reads raw bytes from the radar and extracts sweeps from this data is multithreaded so that reading data and constructing a sweep is separated from the code that returns a sweep array to the Python program. This increases the plot rate because the data capture can occur while the Python program is processing and plotting the previous sweep.
A block diagram of the software architecture is shown in Figure 54.
See the main repo's usage section for how to use the software.
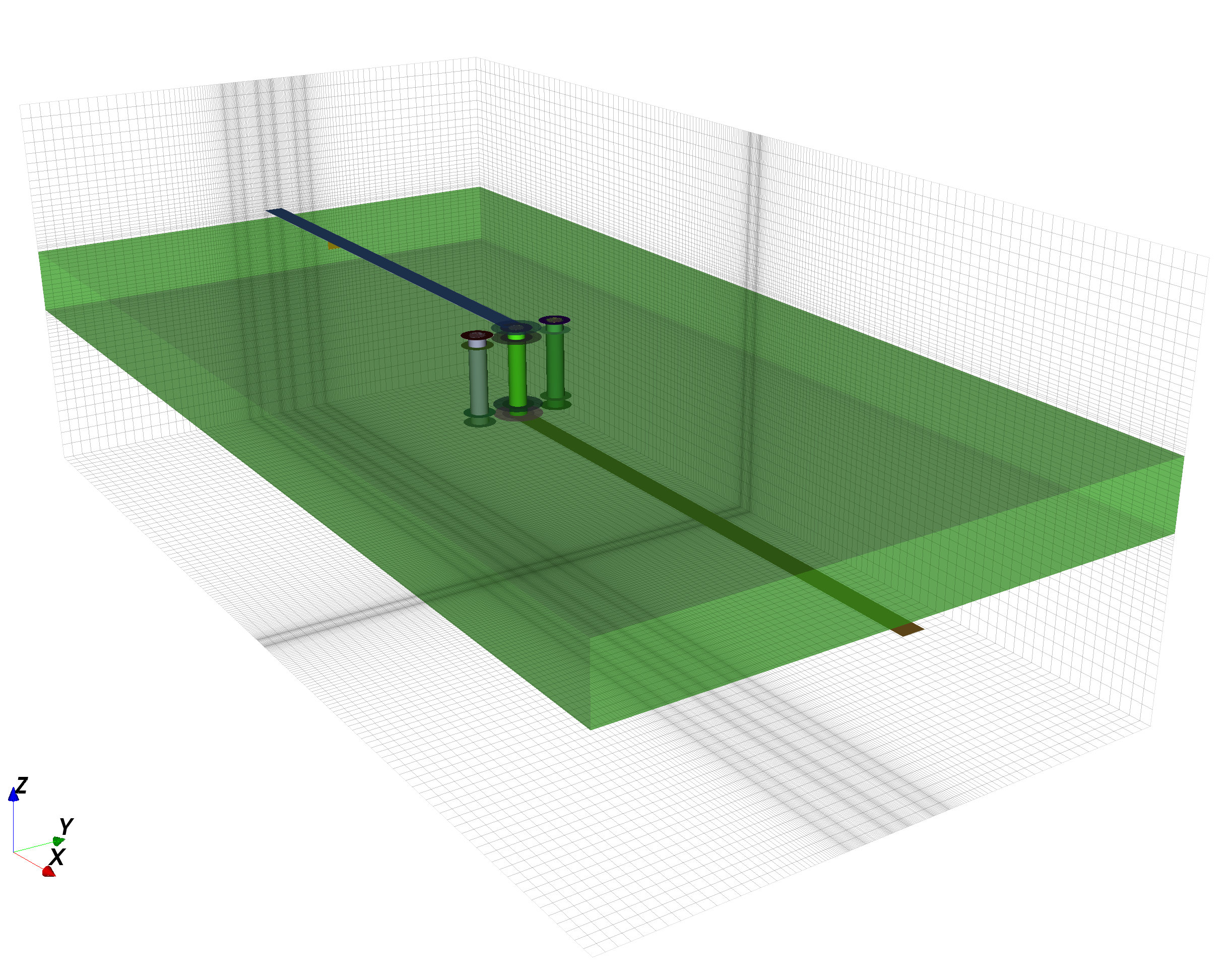
8. RF Simulations
When dealing with low-frequency electronics (and/or sufficiently short conductors), we're able to use a number of approximations that make our analysis much simpler. These approximations are collectively known as the lumped-element model. However, when we get to higher frequencies these assumptions no longer generate good approximations, and instead we have to deal with the underlying physics more directly. In these cases we use a distributed-element model (which employs calculus to reframe electrically-large circuit elements in terms of a lumped-element model) or use simulation tools to compute Maxwell's equations directly.
The radar's transmitter and receiver, which operate in the
Additionally, I wrote a Python driver for OpenEMS that automatically generates a high-quality mesh (a 3-dimensional rectilinear grid specifying where Maxwell's equations should be evaluated at each discrete timestep) from a physical structure. It also provides a number of other useful capabilities such as the ability to optimize some arbitrary part of a structure for a desired result. All of my simulations use this tool and are available in the main radar repo.
8.1. Microstrip Transmission Line
The radar primarily employs microstrip transmission lines to transmit high-frequency AC signals on the PCB. Transmission lines become necessary whenever the phase of the signal conducted by the transmission line varies appreciably over the length of that line. This can occur either when the signal is of sufficiently high-frequency, or when the transmission line is sufficiently long. In our case it is due to high signal frequencies.
A microstrip is a very common form of transmission line that employs a signal trace on the surface of a PCB and an unbroken ground plane beneath it. A cross section of this is presented in Figure 55.
All of the microwave ICs have their input and output impedances internally matched to
The reason impedance matching is critical is expounded in the theory section. The actual simulation and analysis are presented in the simulation section.
8.1.1. Theory
Next high-level section: Simulation
Matching the characteristic impedance of a transmission line to the source and load impedance limits signal reflections on the transmission line and maximizes power transfer to the load. Signal reflections due to impedance discontinuities cause signal power to return to the source, which limits the power transmitted to the load and can potentially damage the source. I'll discuss this more at the end of the section, but first it's helpful to develop some transmission line theory.
Let's analyze why impedance discontinuities cause signal reflections. It's worth mentioning that the following discussion does not directly address the original question as to why the transmission lines need to have their characteristic impedance matched to the source and load impedance. Rather, it looks at the closely-related situation in which a mismatched load causes signal reflections. Nonetheless, it's an easy step from this to understanding why impedance-matched transmission lines are important.
Transmission lines have distributed inductance, capacitance, resistance and admittance over their length. Because the voltage signal traversing the transmission line does not have the same value everywhere along the line, we can no longer lump all of this into a single inductor, capacitor and 2 resistors connected by perfect, delay-free conductors. However, we can restrict ourselves to a short enough segment of the transmission line over which all of these values can be lumped. This short segment, with length
For sufficiently short transmission lines (as in our case) we can neglect the resistive components and our model simplifies to Figure 57.
The complete transmission line of length
The characteristic impedance, which is the instantaneous ratio of voltage to current anywhere along the transmission line assuming no reflections, is given by
| (8.1.1.1) |
This result is not especially difficult to derive, but since the derivation is done elsewhere4 I won't perform it here.
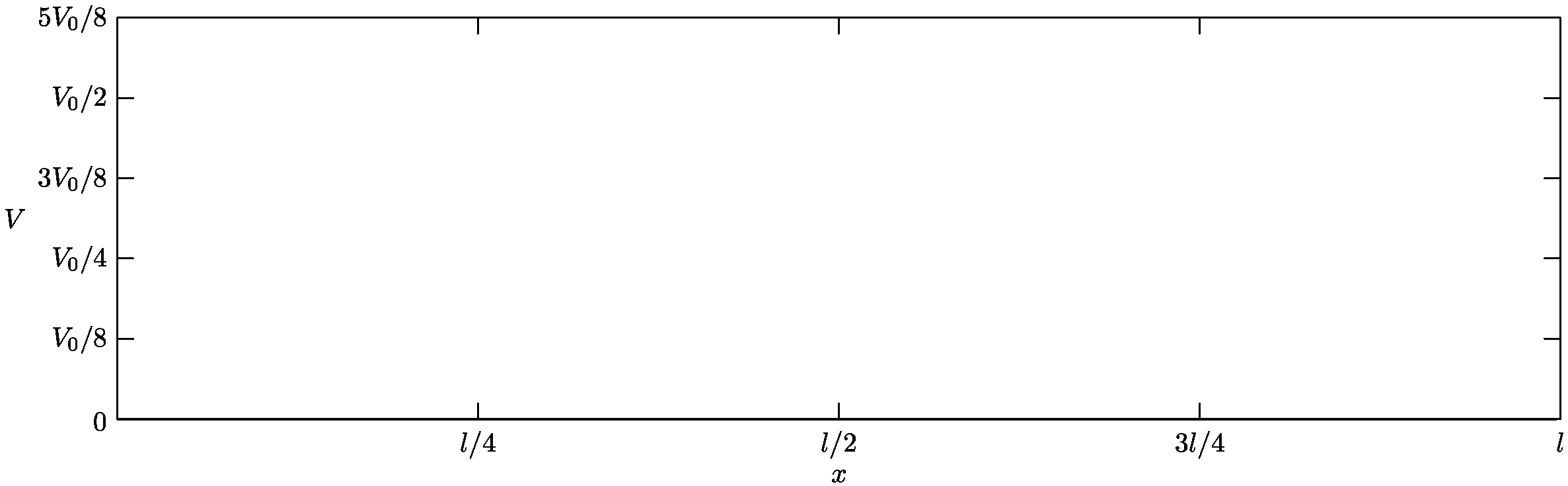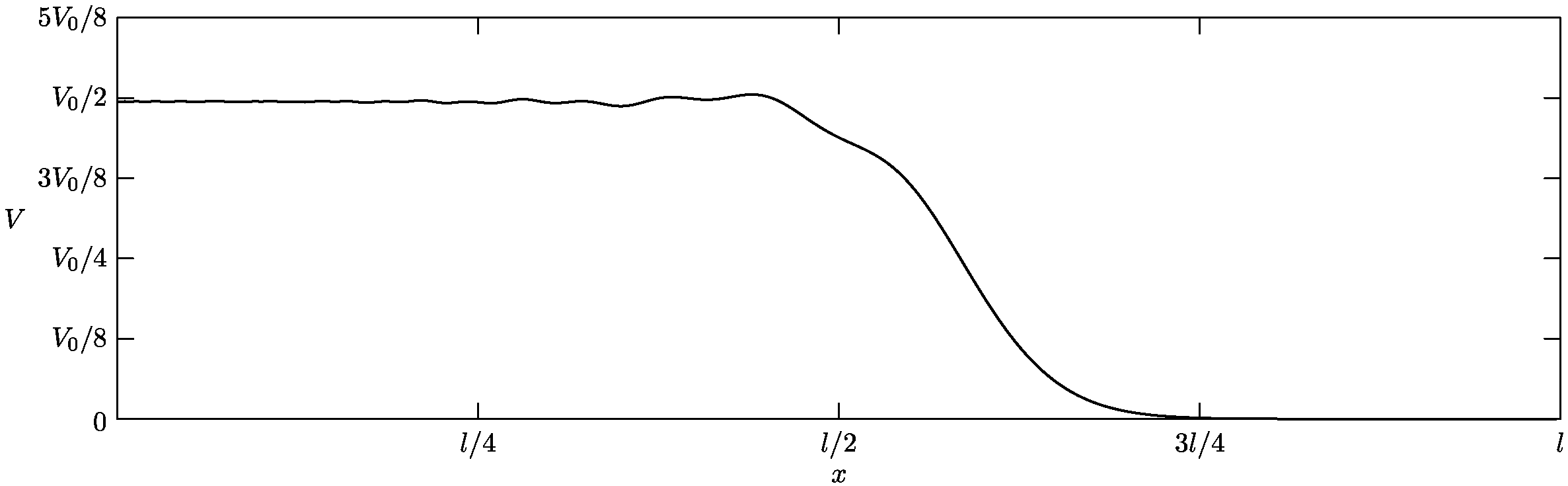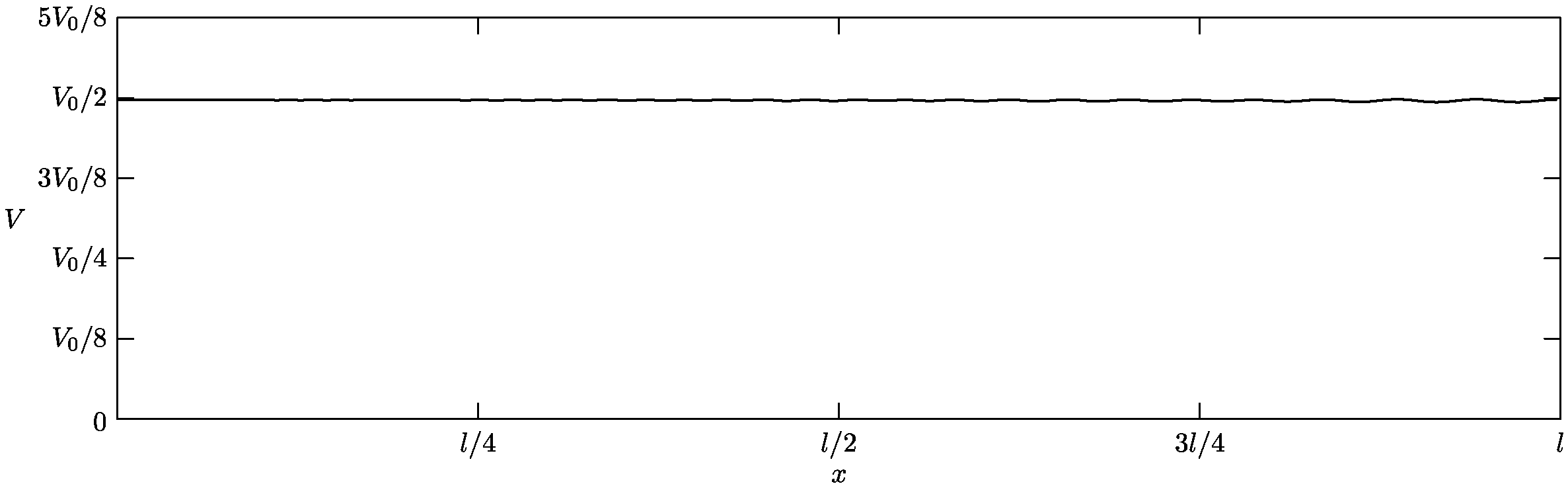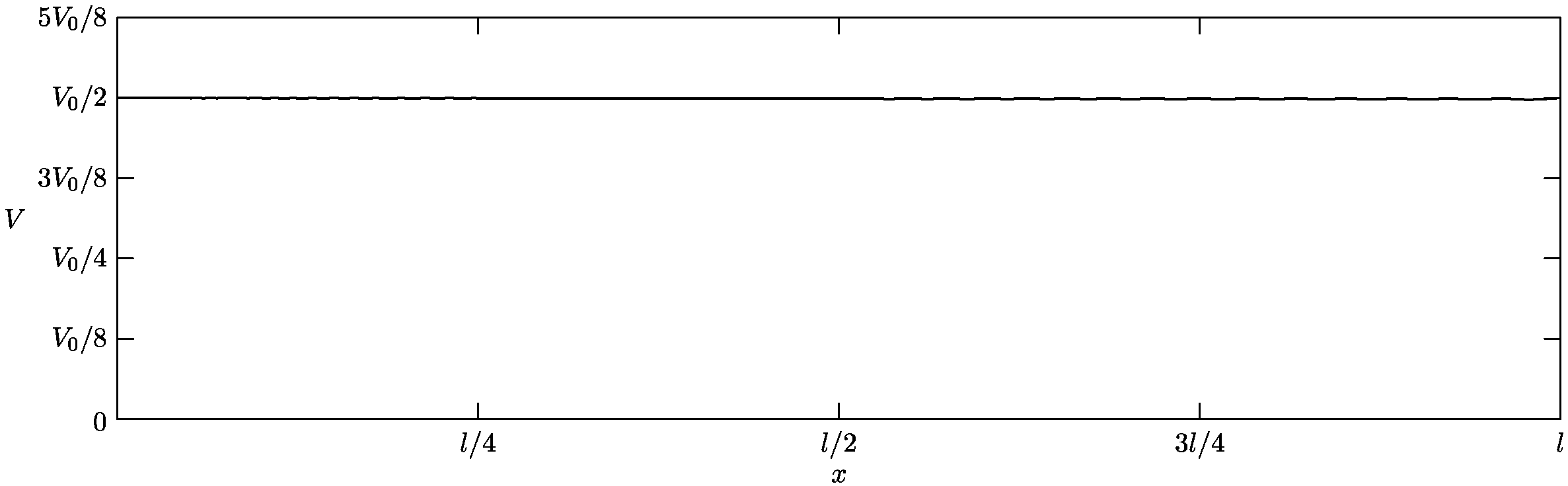
To understand how a signal propagates down this transmission line and why impedance discontinuities present signal reflections, imagine the voltage source creates a pulse with the pulsed voltage equal to
When we reach the last capacitor (in parallel with the load), we find that if the load impedance is equal to
To illustrate the effect of a mismatched load I've simulated the LC network approximation of a transmission line using Ngspice. The voltage source creates a pulse that propagates down the line. The source resistance is
Now, I'll return to the topic of why signal reflections actually matter. Instead of a pulse, let's take a single-frequency sinusoid propagating down a transmission line. Let's start by investigating a case where the end of the transmission line is short-circuited. The SWR Wikipedia page has a great visualization of this, which I've presented in Figure 61.
Figure 61: Incident (blue) and reflected (red) voltages and the resulting standing wave (black) produced by a transmission line terminated in a short circuit (point furthest to the right). This animation has been taken from Wikipedia where it is in the public domain.
The red dots conveniently show the nodes, or the locations where the incident and reflected waves are always
The reason why a load impedance mismatch causes less energy to reach the load is due to something related to but subtly different from the phenomenon of reflections on a transmission line. It is described by the maximum power transfer theorem, which states that for a finite source impedance, the load impedance which maximizes power delivered to the load is the complex conjugate of the source impedance. It's worth emphasizing this fixed nature of the source impedance, because if you can change the source impedance, you will always increase power delivery to the load by decreasing source impedance. Let's restrict ourselves to strictly real impedance values (that is, resistance values) from now on. A way to think about this theorem conceptually is that even though increasing the load resistance above the source resistance will increase the proportion of the voltage dropped across the load in comparison with the voltage dropped across the source, the total resistance will also increase, decreasing the current through the source and the load. So, increasing the load resistance increases the efficiency, but decreases the total power delivery. The power delivered to the load is
| (8.1.1.2a) | ||||
| (8.1.1.2b) |
From calculus we know that the local maximum or minimum will occur where
The derivative of the power delivered to the load with respect to the load resistance is
| (8.1.1.3) |
| (8.1.1.4a) | ||||
| (8.1.1.4b) |
The first case corresponds to
Finally, it might be tempting to think that this source-load impedance matching requirement would necessitate wasting 50% of the energy at each stage. This is not the case. For instance, power amplifiers are typically designed to present a
8.1.2. Simulation
When determining the correct width of a microstrip trace to match a desired characteristic impedance, an engineer will often use an approximate equation rather than a full-blown electromagnetic wave simulator. These provide a fairly good approximation for microstrips, which are comparitively simple structures. Although different approximations tend to differ by several ohms from one another, this isn't critical because PCB manufacturers' tolerances tend to be the limiting factor. For instance, even PCB manufacturers that provide controlled-impedance (OSHPark, which this project uses, does not) often only guarantee to be within
The microstrip characteristic impedance over a sweep of trace widths is shown in Figure 62. This is a capability of pyems, which is able to sweep across arbitrary input simulation parameters and perform each simulation in its own process to leverage the multicore nature of most CPUs. The result tells us that we should use a microstrip trace width of
The microstrip transmission line model assumes that there is no coplanar ground plane or ground fill (a ground plane on the same copper layer as the signal trace, shown in Figure 63). This is usually a false assumption because coplanar ground planes plus via fences provide excellent isolation from surrounding traces. The trick is to ensure the coplanar ground plane is far enough away such that most of the field lines are between the adjacent layer ground plane and signal trace instead of the coplanar ground plane and signal trace. Otherwise, you've inadvertently constructed a grounded coplanar waveguide, which will have a somewhat different impedance than the microstrip. We could use a grounded coplanar waveguide instead of the microstrip, but they require narrow gaps between the trace and coplanar ground plane and are therefore more sensitive to manufacturer's tolerances.
To determine the necessary separation, we can gradually move the coplanar ground plane further away from the trace and see at what point further movements of the plane no longer have an appreciable effect on characteristic impedance. Equivalently, we can find the minimum gap for which the characteristic impedance is approximately equal to the characteristic impedance we found in Figure 62. I've performed a sweep of the gap between the signal trace and ground plane. The gap is presented as a proportion of the trace width so that we see how many trace widths separation we need. The results are shown in Figure 64.
The simulation results indicate that if the gap width is roughly the same size as the trace width or larger, the coplanar ground plane has little discernable effect on the characteristic impedance of the microstrip.
8.1.2.1. Differential Microstrip
A differential microstrip consists of two identical signal traces separated by a fixed-width gap, as shown in Figure 65. Like a traditional microstrip, there is an uninterrupted ground plane on the adjacent copper layer. The narrow gap between the traces causes some energy to pass between the traces. This is desirable because it means common-mode noise will affect the signal on each trace equally. The differential amplifier that amplifies the differential signal at the input to the next device will have a high common-mode rejection ratio (CMRR) and therefore most of the common-mode noise will be removed.
To keep the coupling factor high, it is important to keep the gap between the traces small. I've used
If there were no coupling between the traces, we could simply set the trace width equal to the width for a single microstrip trace with characteristic impedance equal to half the desired differential impedance. However, coupling has the effect of lowering the differential impedance, so the trace width needs to be narrower than the
8.2. Horn Antenna
I made 3D-printed horn antennas using the instructions given here. I generated the STL files using OpenSCAD modelled after the Pasternack PE9860-15 antenna. The OpenSCAD code file is included in the main FMCW repository. The simulation structure is shown in Figure 67. A time lapse of the electric field propagation through air due to an excitation of the waveguide in the antenna is shown in Figure 68.
Figure 67: OpenEMS horn antenna structure. The horn structure is created from an STL file, and the waveguide port and mesh are generated by pyems.
The simulated return loss is less than
The plots in Figure 70 show that the radiation pattern has a beamwidth of about
This is a good directivity value for our target range and demonstrates one of the desirable characteristics of horn antennas, in addition to having a large bandwidth. Having a high directivity value means that a larger percentage of the radiated energy is concentrated in the direction we're pointing the antenna. This is highly desirable for most radars since it increases their range and angular resolution at the cost of needing to pivot the antenna to see in other directions (antenna arrays can do this without pivoting, by injecting deliberate delays to each array element). This might give the impression that directivity is always good but that's not the case. For instance, if a cell phone antenna had high directivity, it would mean that we'd get much better service if we were facing one way than another way, which is obviously not what we want. To that effect, cell phone antennas are designed for as low a directivity as possible. On the other end of the spectrum are dish antennas which have very high directivity and are thus used for very long range applications.
8.3. Directional Coupler
The simplest implementation of a directional coupler (and the implementation used in this design) involves two tightly-spaced microstrip lines. The signal is passed into one end of one of the microstrips, and most of the energy passes through to the other end of the same microstrip. However, some of the energy is coupled into the adjacent microstrip. The amount of coupled energy is inversely related to the separation between the lines, which we can control to achieve a desired energy coupling over a target frequency range.
The maximal coupling between the lines occurs when the line length is a multiple of
A bird's-eye view of the simulated coupler structure is shown in Figure 71.
Figure 71: Directional coupler structure in CSXCAD. From upper left proceeding clockwise, the port numbers are 1, 2, 4 and 3.
Animation 72 shows the magnitude of the current density over time for an excitation at port 1.
Figure 72: Animation of the current density magnitude over time for the simulated directional coupler.
The simulation results are shown in Figure 73.
The simulation results exhibit the desired coupling factor within the bandwidth of interest. The directivity, on the other hand, is fairly poor. However, as described in the theory section, that does not matter much here. If we had needed a larger bandwidth and/or better directivity, there are many ways to do this.5
8.4. SMA connector
The radar uses a Mueller SMA connector, which is low in cost but still provides good performance in our target frequency range. The simulation structure is shown in Figure 75.
I've plotted the S-parameter performance of the microstrip to SMA transition from DC to
8.5. RF Via
A previous iteration of the PCB used an RF via to carry the transmission signal back to the receiver. Although the updated PCB keeps this signal on the top layer, it is worth keeping this section to characterize the behavior of the previous PCB.
Vias change the per-unit-length inductance and capacitance of transmission lines. This is not surprising because the via plating typically has a different surface area than the microstrip trace and the transmission line no longer has a backing copper plane to act as the current return path. The absence of a nearby reference plane decreases the capacitance and thus increases the characteristic impedance of the via. A good way to compensate for this effect is to place vias tied to the reference plane adjacent to the signal via. This construction is shown in Figure 77.
Figure 77: High-frequency via for transitioning signals between the top layer and bottom layer. I've removed the first and last substrate layers as well as the second and third metal layers from the image in order to make the remaining structures easier to see. These omitted structures exist in the actual simulation.
This RF via structure takes inspiration from Henrik's design (see this post). However, I've made an important change: Henrik uses the via to transition the signal between layers 1 and 3, whereas I transition between layers 1 and 4. His construction transitions from a microstrip on the top layer to an asymmetric stripline on the 3rd layer. The main difference between the asymmetric stripline and the microstrip is that the microstrip is bounded by two different dielectrics (the substrate and air), whereas the stripline is bounded by the substrate above and below. In regard to the proximity to the ground reference plane, layers 2 and 3 are much farther apart than layers 3 and 4, so in this way it should behave like a microstrip. If the performance criteria were stringent, it would probably be a good idea to independently characterize the stripline. However, given the comparatively low frequency range of our signal and the manufacturer's tolerance limitations, the performance difference won't matter and so the stripline could be made the same width as the microstrip.
The simulated RF via S-parameters are shown in Figure 78. This performance is more than adequate in our frequency range of interest, and indeed works quite well even up to much higher frequencies.
8.6. Series Blocking Capacitor
Several of the radar's transmission lines require a DC blocking capacitor. In an ideal world, adding a series capacitor would simply amount to embedding a large series capacitance into our lumped-element transmission line model. However, this would generate misleading results for several reasons. First and most importantly, capacitors have complicated internal structures that have a significant effect on their frequency response. Additionally, this will ignore mounting considerations: for instance, impedance discontinuities due to the capacitor and its pads having a different width than the microstrip trace. Lastly, if our max frequency is sufficiently high, the capacitor will no longer appear electrically small and cannot be modelled as a lumped-element. This last effect isn't particularly relevant here since the capacitor is still small at
Although OpenEMS can model lumped elements, doing so would ignore the capacitor's internal structure. Theoretically, if we knew the capacitor's internal structure we could simulate it with OpenEMS, but we'd never want to do this because the simulation would take too long. Fortunately, Murata, which manufactures the high-frequency capacitors I've used in the design, has tested the frequency response of their capacitors with a VNA and made all the information publically-available online. We can use this result directly. This will ignore mounting effects because the simulation data only includes the frequency response of the capacitor.
Typically, a larger capacitor than microstrip width is compensated by removing a small rectangle of ground plane beneath the capacitor. This works because the larger capacitor width increases the lumped-element capacitance and reduces the lumped-element inductance for the length-duration of the capacitor. By removing a section of ground plane beneath the capacitor, we are reducing the capacitance and increasing the inductance. This uses the same principles as a miter, except that with a miter we remove part of the top trace instead of the ground plane. In any event, this compensation technique won't work because this design uses a 0201 capacitor whose width (
The performance of the 0201 capacitor is notably better at
9. Footnotes
Footnotes:
I actually have an upgrade planned for it that should make the angle detection more precise than the original version. I've developed a PCB for it but haven't tested it or written the FPGA code or software to support it yet.
S. He and M. Torkelson. A New Approach to Pipeline FFT Processor. 1996.
C. Cummings. Simulation and Synthesis Techniques for Asynchronous FIFO Design. 2002.
D. Pozar. Microwave Engineering, Fourth Edition. Section 2.1: The Lumped-Element Circuit Model For A Transmission Line.
In particular, RF and Microwave Coupled-Line Circuits (Mongia, 1999) discusses numerous ways to design directional couplers with these goals in mind.